La energía total de un satélite que describe una órbita circular es:
![]()
siendo r el radio de la órbita, M la masa del astro alrededor del cual gira el satélite, y m la masa del satélite. Por otro lado, la energía total es suma de la energía cinética más la potencial:
ET=EC+EP ⇒ EP=ET-EC
Por ser una órbita circular, la única fuerza que se ejerce sobre el satélite es la de atracción gravitatoria, en dirección radial y apuntando hacia el centro de la órbita. Y como el movimiento es circular y uniforme, la única aceleración que tendrá es la normal o centrípeta, de la misma dirección y sentido que la fuerza de atracción gravitatoria. Aplicando entonces la segunda ley de Newton:
![]()
Sustituyendo entonces en la expresión de la energía potencial:
![]()
![]()
Dividiendo las energías total y potencial:
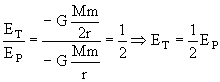
![]()