Menos tiempo al bajar deslizando

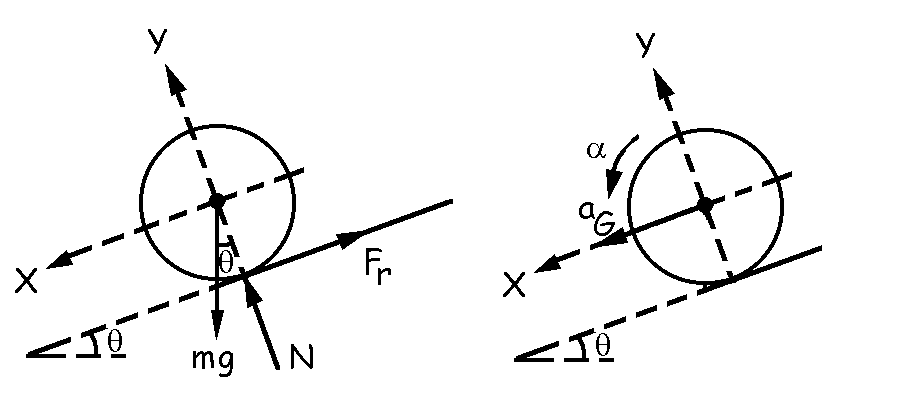
Puesto que la inclinación del plano y la velocidad inicial del cuerpo son las mismas en ambos casos, caerá más deprisa aquél que tenga mayor aceleración. Empecemos por determinar la aceleración que tendrá el cuerpo que cae rodando. Trazamos en primer lugar el diagrama de fuerzas. Obviamente tiene que existir una resistencia a la rodadura que llamaremos F_r, ya que sin ella el cuerpo no podría rodar. Tomando momentos respecto del centro de masa tendremos:

Además, como rueda sin deslizar se cumplirá que:

Sustituyendo esto en la expresión obtenida a partir de los momentos:

Ahora, aplicando la segunda ley de Newton:

De donde obtenemos la aceleración del centro de masas en este primer caso:

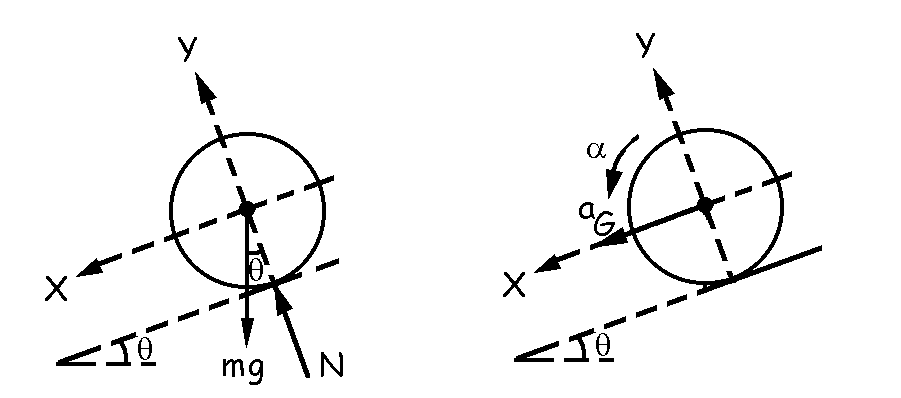Ahora vamos a ver qué ocurre cuando el disco desliza en ausencia de rozamientos. Tendremos en este caso que la única fuerza que actúa sobre él es su propio peso. Aplicando la segunda ley de Newton:

ΣF_X=ma_GX ⇒ mgsenθ=ma_G ⇒ a_G=gsenθ

Podemos ver que la aceleración del centro de masas es mayor en este segundo caso, luego el cuerpo baja más deprisa cuando baja deslizando.

MENOS TIEMPO AL BAJAR DESLIZANDO