d=60cm
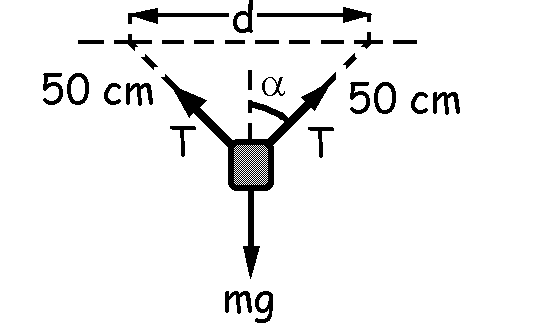
Hacemos el diagrama de sólido libre de la pesa con las anillas. La pesa estará sometida a su peso y a la tensión ejercida por las cuerdas que van a cada anilla. Tal como hemos denominado a los parámetros geométricos en la figura la máxima separación d entre las anillas es:
d=50senα+50senα=100senα
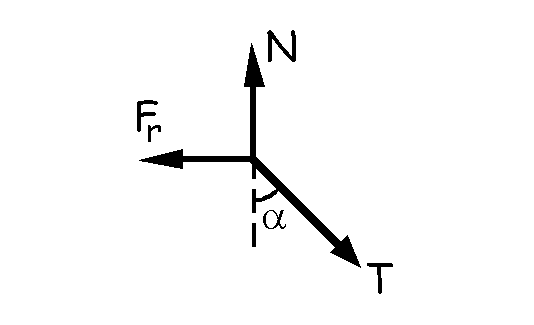 Si ahora hacemos el diagrama de una de las dos anillas, que supondremos sin masa, tendremos lo que aparece en la figura. Cada anilla estará sometida a la tensión del hilo, a la fuerza de rozamiento, y a la reacción normal que ejerce la barra sobre la anilla. Si llamamos eje X al que tiene la dirección de la barra y eje Y al perpendicular se verificará que:
Si ahora hacemos el diagrama de una de las dos anillas, que supondremos sin masa, tendremos lo que aparece en la figura. Cada anilla estará sometida a la tensión del hilo, a la fuerza de rozamiento, y a la reacción normal que ejerce la barra sobre la anilla. Si llamamos eje X al que tiene la dirección de la barra y eje Y al perpendicular se verificará que:
ΣFx=0 ⇒Tsenα-Fr=0
ΣFy=0 ⇒N-Tcosα=0 ⇒ N=Tcosα
En el instante en que d es máximo las anillas están a punto de deslizar, luego la fuerza de rozamiento adquiere su valor máximo:
Fr=(Fr)máx=µN=µTcosα
Sustituyendo esto en la ecuación del eje X:
ΣFx=0 ⇒ Tsenα-Fr=0 ⇒ Tsenα-µTcosα=0 ⇒ senα-µcosα=0 ⇒
![]()
Si elevamos esa expresión al cuadrado:
![]()
Además sabemos que:
sen2α+cos2α=1
De la primera expresión:
![]()
Y sustituyendo en la segunda:
sen2α+cos2α=1 ⇒ 0.5625 cos2α+cos2α=1 ⇒ 1.5625cos2α=1 ⇒ cosα=0.8 ⇒
α=36.87º
Y por tanto la distancia máxima d que se pueden separar las anillas es:
d=100senα
=100sen36.87º=60 cm
d=60cm