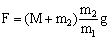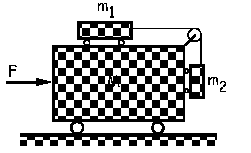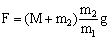
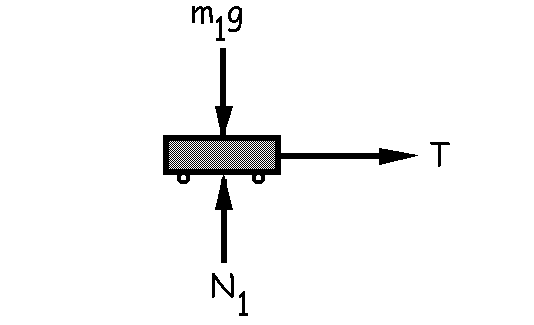
 Si m1 y m2 no se mueven con respecto al M quiere decir que todos los cuerpos se mueven con la misma aceleración a. A lo largo de todo el problema llamaremos eje X al eje horizontal (positivo hacia la derecha) y eje Y al eje vertical (positivo hacia arriba). Aislando el bloque de masa m1 tendremos:
Si m1 y m2 no se mueven con respecto al M quiere decir que todos los cuerpos se mueven con la misma aceleración a. A lo largo de todo el problema llamaremos eje X al eje horizontal (positivo hacia la derecha) y eje Y al eje vertical (positivo hacia arriba). Aislando el bloque de masa m1 tendremos:
ΣFX=m1a1X ⇒ T=m1a
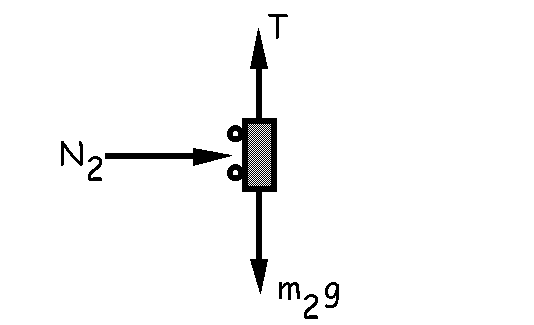 A continuación aislamos el cuerpo de masa m2, para el que haciendo lo mismo tendremos:
A continuación aislamos el cuerpo de masa m2, para el que haciendo lo mismo tendremos:
ΣFX=m2a2X ⇒ N2=m2a
ΣFY=m2a2Y ⇒ T-m2g=0 ⇒ T=m2g
Sustituyendo la tensión en la expresión que habíamos obtenido a partir del bloque m1:
T=m1a ⇒ m2g=m1a
 Por último aislamos el bloque de masa M y tendremos:
Por último aislamos el bloque de masa M y tendremos:
ΣFX=MaX ⇒ F-N2=Ma
Sustituimos N2 por su valor, obtenido mediante las ecuaciones del bloque 2:
F-N2=Ma ⇒ F-m2a=Ma ⇒ F=(M+m2)a
Y la aceleración podemos determinarla a partir de las ecuaciones del bloque 1:
![]()
Con lo cual la fuerza F vale:
![]()