Cuestion de Dinámica de la Partícula

Un bloque de 5 kg comienza a subir por un plano inclinado 30o con una velocidad inicial de 20 m/s. a) ¿Qué distancia recorrerá sobre el plano antes de detenerse si el coeficiente cinético de rozamiento vale 0.25? b) Sea 0.45 el coeficiente estático de rozamiento. ¿Volverá a bajar el bloque después de haberse detenido? En caso afirmativo, ¿cuál será su velocidad al llegar de nuevo al pie del plano?

a) e=28.48 m
b) Volverá a bajar; vF=12.58 m/s

a) En primer lugar hacemos el diagrama de sólido libre del cuerpo.

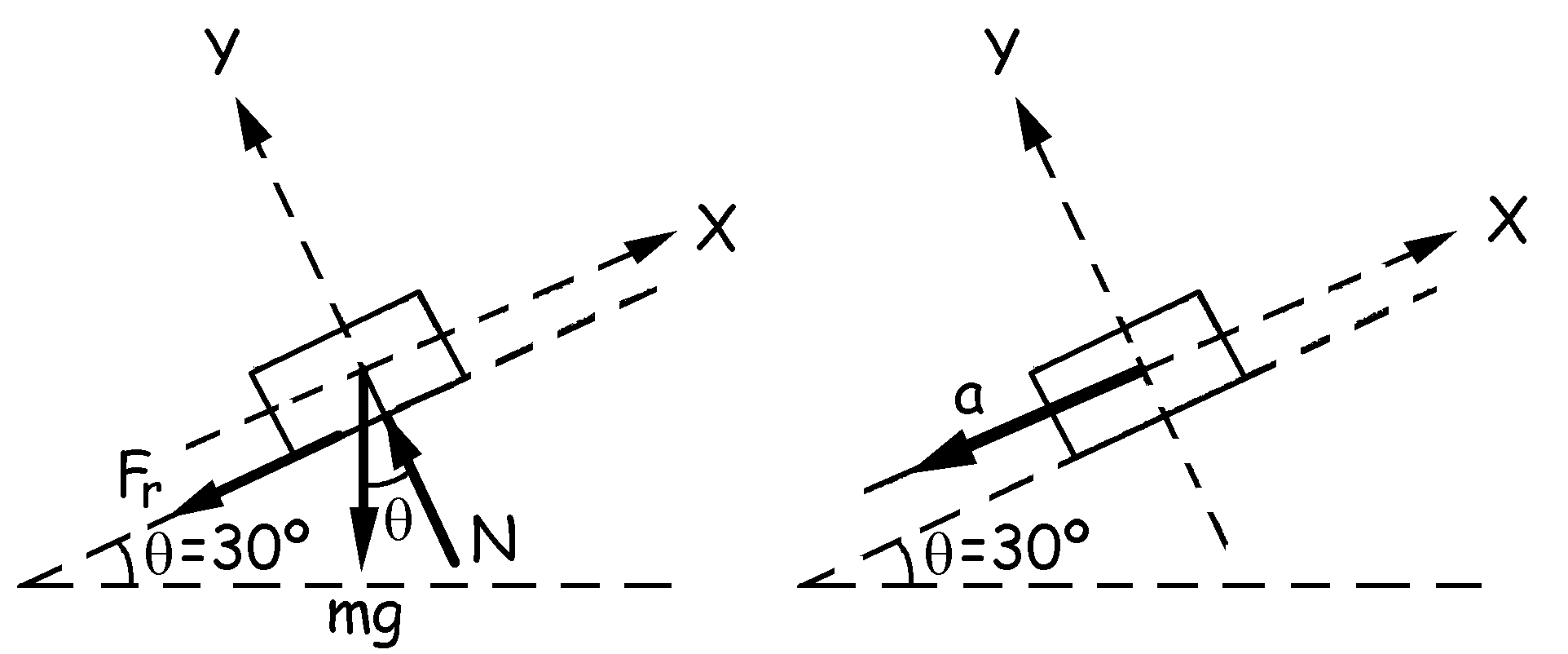
Aplicando la segunda ley de Newton tendremos:

ΣFy=may ⇒ N-mgcosθ=0 ⇒ N=mgcosθ

ΣFx=max ⇒ mgsenθ+Fr=max ⇒ mgsenθ+µcN=max ⇒ mgsenθ+µcmgcosθ=max

ax=gsenθ+µCgcosθ=9.8sen30º+0.25 · 9.8cos30º=7.02 m/s2

Como el movimiento es rectilíneo uniformemente decelerado tendremos:

e=28.48 m

 

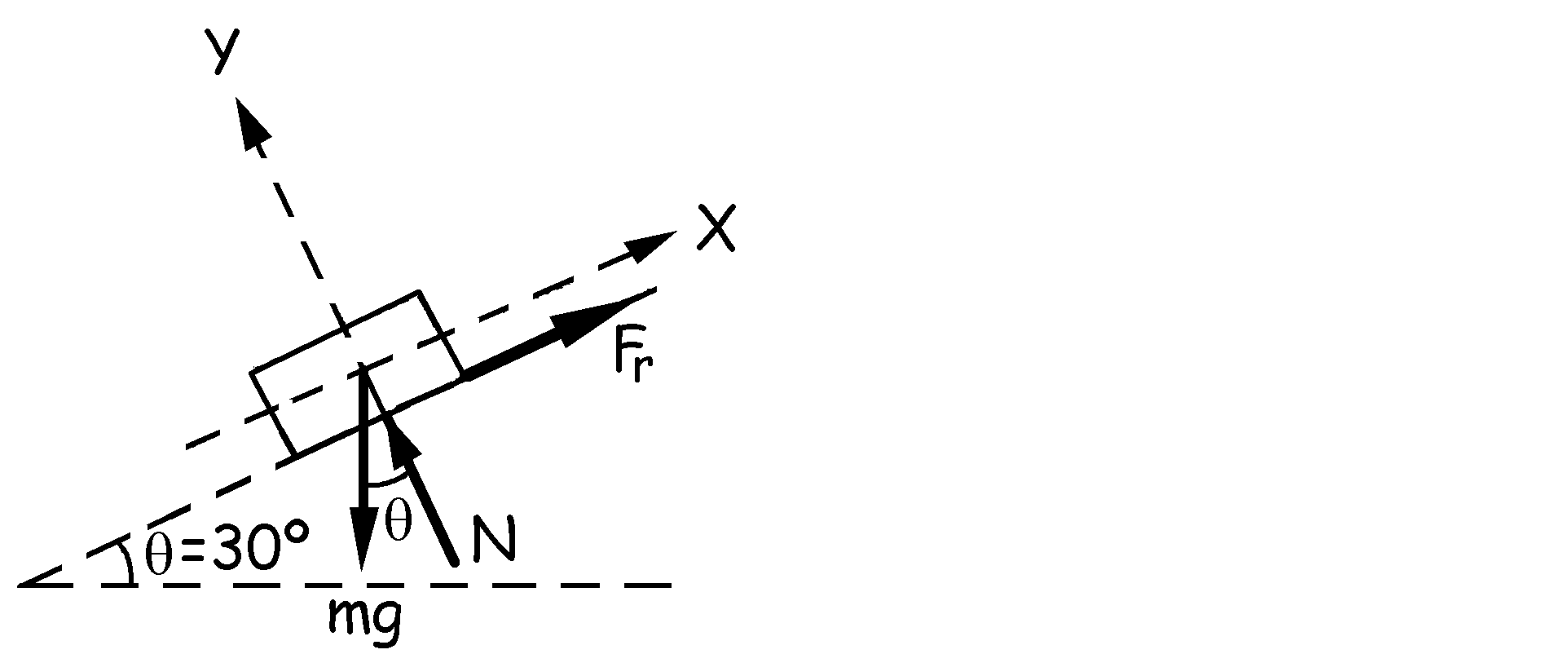b) Tracemos ahora el diagrama de sólido libre del cuerpo en el instante en que se detiene. El cuerpo volverá a bajar si la componente del peso es mayor que la fuerza máxima de rozamiento estático. Entonces:

Px=mgsenθ=5 · 9.8sen30º=24.5 N

(Fr)máx=µeN

Y la normal valdrá, aplicando la segunda ley de Newton:

ΣFy=may ⇒ N-mgcosθ=0 ⇒ N=mgcosq

Entonces:

(Fr)máx=µeN=µemgcosθ=0.45 · 5 · 9.8cos30º=19.10 N

Como la componente del peso es mayor que la fuerza máxima de rozamiento, el cuerpo volverá a bajar.

VOLVERÁ A BAJAR

 

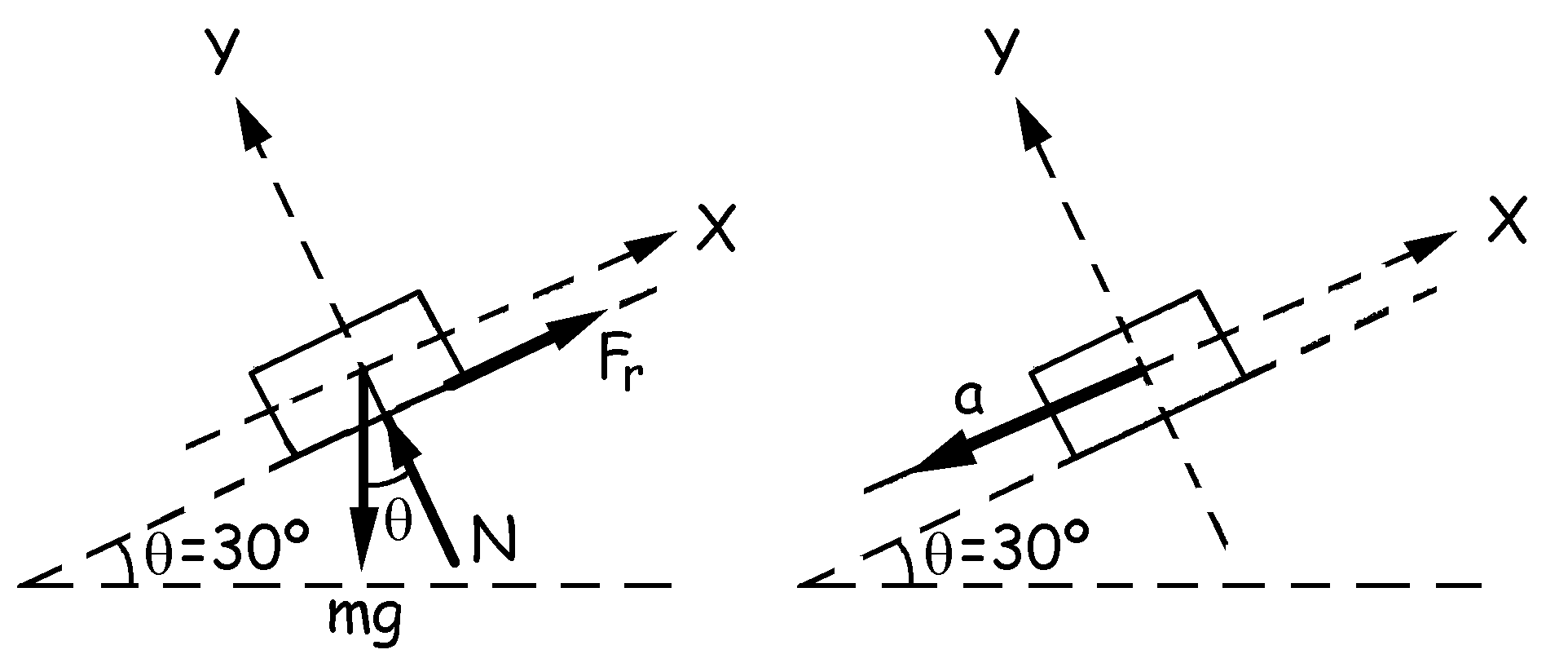Volvemos a hacer de nuevo el diagrama de sólido libre del cuerpo en este caso cuando está bajando. Aplicando de nuevo la segunda ley de Newton:

ΣFy=may ⇒ N-mgcosθ=0 ⇒ N=mgcosθ

ΣFx=max ⇒ mgsenθ-Fr=max ⇒ mgsenθ-µcN=max ⇒ mgsenθ-µcmgcosθ=max

ax=gsenθ-µCgcosθ=9.8sen30º-0.25 · 9.8cos30º=2.78 m/s2

 

Como todas las fuerzas que actúan sobre el cuerpo son constantes, la aceleración también lo es, luego el movimiento es rectilíneo uniformemente acelerado. Tendremos pues:

vF=12.58 m/s