N1=mgcosα; N2=mgsenα; tgΦ=cotg2α
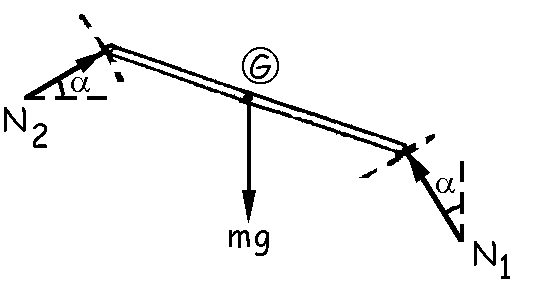 Trazamos el diagrama de sólido libre de la varilla, donde aparecerán únicamente las reacciones normales N1 y N2 y el peso de la varilla. Tomaremos como eje X el horizontal, positivo hacia la derecha, y como eje Y el vertical, positivo hacia arriba. Aplicando las condiciones de equilibrio tendremos:
Trazamos el diagrama de sólido libre de la varilla, donde aparecerán únicamente las reacciones normales N1 y N2 y el peso de la varilla. Tomaremos como eje X el horizontal, positivo hacia la derecha, y como eje Y el vertical, positivo hacia arriba. Aplicando las condiciones de equilibrio tendremos:
ΣFX=0 ⇒-N1senα+N2cosα=0
ΣFY=0 ⇒ N1cosα+N2senα-mg=0
De la ecuación del eje X:
![]()
Sustituyendo esto en la ecuación del eje Y:
N1cosα+N2senα-mg=0 ⇒N1cosα+N1tgαsenα=mg ⇒
![]()
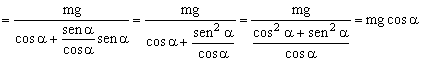
N1=mgcosα
Ahora la otra reacción será:
N2=N1tgα=mgcosαtgα =![]()
N2=mgsenα
Y por último, para determinar la posición de equilibrio, tomamos momentos respecto del centro de masas:
ΣMG=0
![]()
Simplificamos la longitud de la barra y sustituimos las normales por sus respectivos valores:
-mgsenαcosαsenΦ-mgsenαsenαcosΦ-mgcosαsenαsenΦ+mgcosαcosαcosΦ=0
-senαcosαsenΦ-senαsenαcosΦ-cosαsenαsenΦ+cosαcosαcosΦ=0
-2senαcosαsenΦ+cosΦ(cos2α-sen2α)=0 ⇒ 2senαcosαsenΦ=cosΦ(cos2α-sen2α)=0
![]()
