a) ΔyM=6.5·10-4 m; Δym=6.5·10-4 m
b) y3=1.625 mm; y5=3.25 mm
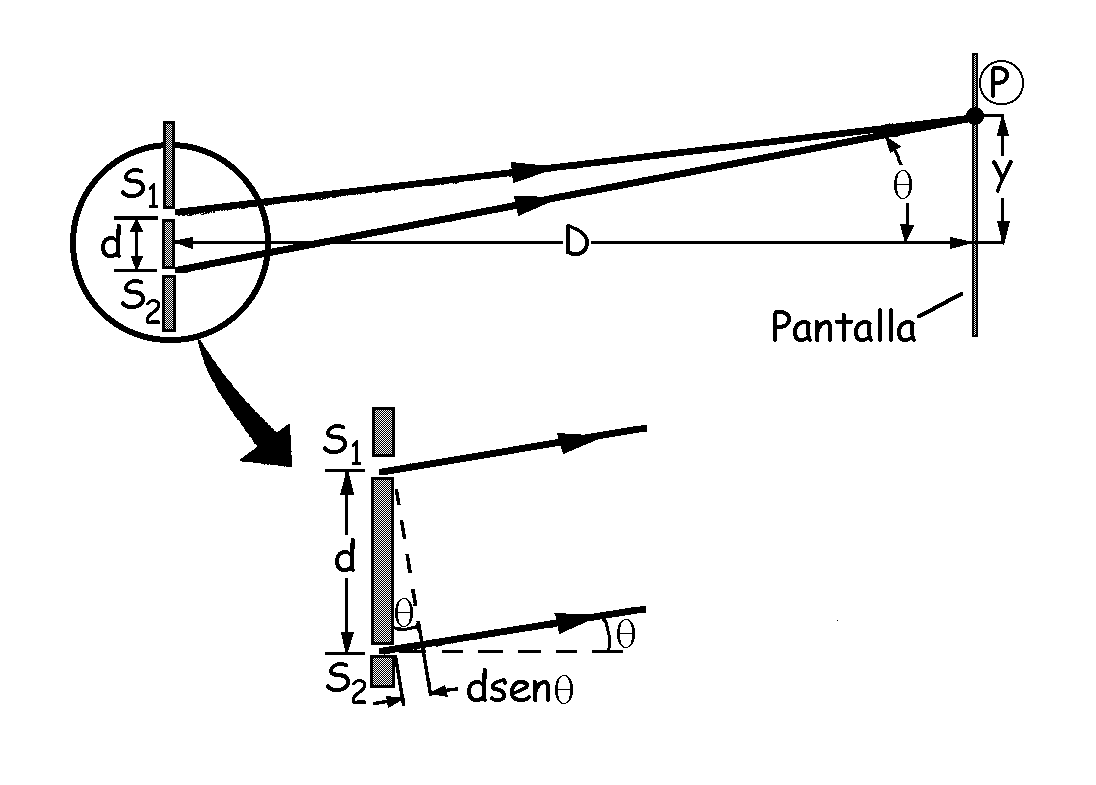 a) En el experimento de Young de la doble rendija tenemos dos rendijas muy estrechas que actúan como fuentes lineales. El diagrama de interferencia se observa sobre una pantalla alejada una distancia D grande en comparación con la distancia d entre las rendijas. A distancias muy grandes de las rendijas, las líneas que van desde las mismas a un cierto punto P sobre la pantalla son aproximadamente paralelas y la diferencia de trayectos es aproximadamente dsenθ, como puede verse en la figura. Así pues, tendremos máximos de interferencia a ángulos dados por:
a) En el experimento de Young de la doble rendija tenemos dos rendijas muy estrechas que actúan como fuentes lineales. El diagrama de interferencia se observa sobre una pantalla alejada una distancia D grande en comparación con la distancia d entre las rendijas. A distancias muy grandes de las rendijas, las líneas que van desde las mismas a un cierto punto P sobre la pantalla son aproximadamente paralelas y la diferencia de trayectos es aproximadamente dsenθ, como puede verse en la figura. Así pues, tendremos máximos de interferencia a ángulos dados por:
dsenθ=Nλ (N=0, 1, 2, 3, …)
La distancia yM medida a lo largo de la pantalla desde el punto central hasta la M-ésima franja brillante está relacionada con el ángulo θ por:
![]()
donde D es la distancia entre las rendijas y la pantalla. Como el ángulo θ es pequeño:
![]()
De modo que sustituyendo en la ecuación que nos daba los máximos:
dsenθ=Nλ
![]()
Para dos máximos consecutivos:
![]()
Restando las dos expresiones tendremos la separación entre máximos:
![]()
ΔyM=6.5·10-4 m
Del mismo modo, se producirán mínimos cuando:
![]()
Igual que antes podemos relacionar dsenθ con la distancia ym medida a lo largo de la pantalla y llegamos a la ecuación:
![]()
Para dos mínimos consecutivos:
![]()
Restando las dos expresiones tendremos la distancia entre dos mínimos consecutivos:
![]()
Δym=6.5·10-4 m
b) Para la tercera franja oscura tendremos que utilizar la ecuación de los mínimos con N=2:
![]()
y3=1.625 mm
Y para la quinta franja brillante usaremos la ecuación de los máximos con N=5:
![]()
y5=3.25 mm