a) T_Tetis=162957.54 s
b) Δv_A=-4382.08 m/s
c) v_B=9975.92 m/s
d)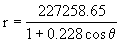
e) β≠132.24^o

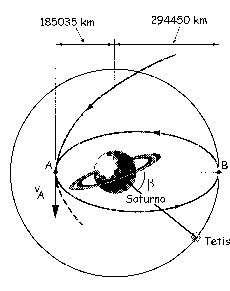
a) Para determinar el tiempo que Tetis tarda en dar una vuelta completa (período T_Tetis) tendremos en cuenta que la órbita es una órbita circular de radio r_B. Por ser circular el movimiento es uniforme, de modo que la única fuerza que existe, la fuerza de atracción gravitatoria, será igual al producto masa por aceleración, siendo la única aceleración la normal o centrípeta. Entonces:

Necesitamos conocer para resolver esa ecuación el producto de constantes GM. Para ello, tendremos en cuenta que la astronave llega al punto A siguiendo una trayectoria parabólica, de modo que la energía total de la órbita es cero:

Sustituyendo esto en la expresión del período:

T_Tetis=162957.54 s

 

b) Ahora vamos a buscar la variación de velocidad que debe sufrir la astronave en el punto A para entrar en la órbita elíptica. El incremento de velocidad será:

Δv_A=v’_A-v_A

Inmediatamente antes del incremento de velocidad la astronave se encuentra en el punto A en una órbita parabólica, con velocidad:

v_A=20254 m/s

Inmediatamente después del incremento de velocidad la astronave se encuentra en el punto A pero en la órbita elíptica. Para esta órbita el eje mayor vale:

2a=r_A+r_B=185035+294450=479485 km

En esta órbita se debe conservar la energía total, luego:

El incremento de velocidad es por tanto:

Δv_A=v’_A-v_A=15871.92-20254=-4382.08 m/s

Δv_A=-4382.08 m/s

 

c) En la órbita se conserva el momento angular entre los puntos A y B. Por tanto:

L_A=L_B ⇒ mr_Av’_Asenφ_A=mr_Bv_Bsenφ_B

siendo φ_A y φ_B los ángulos que en cada momento forman el radio vector con la velocidad. En los puntos A y B el radio vector es perpendicular a la velocidad, luego:

φ_A=φ_B=90º ⇒ senφ_A=senφ_B=1

Entonces:

mr_Av’_Asenφ_A=mr_Bv_Bsenφ_B ⇒ r_Av’_A=r_Bv_B

v_B=9975.92 m/s

 

d) La ecuación de la elipse será del tipo:

Conocemos dos puntos de la cónica:

Dividiendo las dos expresiones:

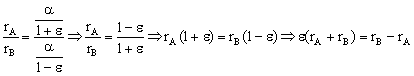
Y la ascensión recta la podemos obtener de una cualquiera de las ecuaciones:

Por tanto la ecuación de la cónica será:

 

e) Podemos determinar el ángulo β necesario para que se produzca el choque, de modo que evitarían el choque todos los ángulo diferentes de ése. Tenemos que la astronave parte del punto A y llega hasta B, en el mismo tiempo en que Tetis recorre el ángulo β. Como el tiempo es común en ambos recorridos, podemos centrarnos en la astronave. Dicho vehículo recorre la mitad de la elipse, luego el tiempo invertido será la mitad del período:

El semieje mayor de la elipse es:

2a=479485 km ⇒ a=239742.5 km

Por tanto:

Ahora pasamos al satélite Tetis, que realiza un movimiento circular uniforme. La velocidad angular será constante, y tenemos que en ese tiempo Tetis recorre un ángulo ⇒ luego:

Con ese ángulo se produce colisión, luego para evitar la colisión el ángulo β deberá ser distinto de ése:

β≠132.24º