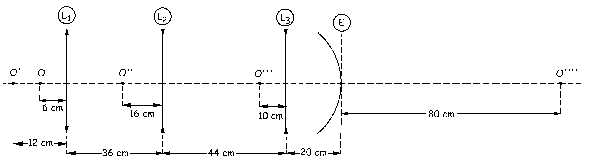
a) R=96 cm; el espejo es cóncavo
a) Llamaremos L1, L2 y L3 a las tres lentes, y E al espejo. Las distancias focales de las lentes serán entonces, teniendo en cuenta si son convergentes o divergentes:
f’1=12 cm; f’2=-24 cm; f’3=-12 cm
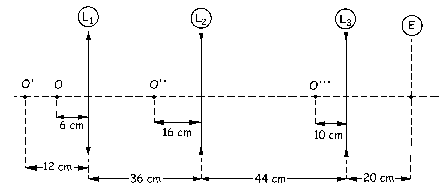
Como no sabemos si el espejo es cóncavo o convexo, representaremos su posición únicamente como una línea discontinua en la posición donde estará situado su vértice. El sistema estará entonces como aparece en la figura, con las tres lentes, el espejo, y el objeto O situado 6 cm a la izquierda de la lente L1.
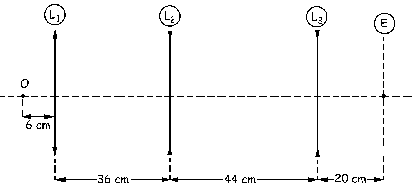
La primera lente en actuar será L1, para la cual el objeto es O y la imagen es O’. Aplicando la ecuación de las lentes:
![]()
Tenemos una distancia imagen negativa, lo que implica que la imagen O’ está situada a la izquierda de L1 y a 12 cm de ella, tal como se muestra en la figura.
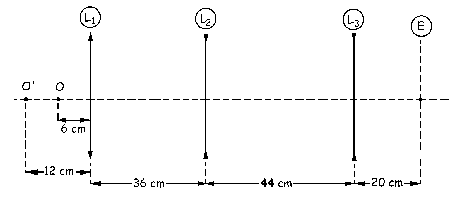
A continuación actúa la lente L2, para la cual el objeto será O’ (imagen dada por el elemento anterior) y la imagen O». Respecto de L2 el objeto O’ está a una distancia de 12+36=48 cm. Aplicando la ecuación de las lentes:
![]()
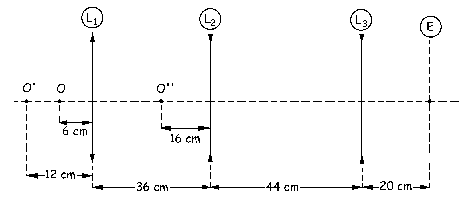
Obtenemos también una distancia imagen negativa, luego la imagen O» está a la izquierda de L2 y a 16 cm de ella.
En tercer lugar actuaría L3, para la cual el objeto es O» y la imagen O»’. Respecto de la lente L3 el punto O»’ está a una distancia de 16+44=60 cm. Aplicamos de nuevo la ecuación de las lentes:
![]()
De nuevo la distancia imagen es negativa, luego el punto O»’ está a la izquierda de L3 y a 10 cm de ella.
Por último actuaría el espejo esférico. Para el espejo el objeto es O»’ y la imagen será O»». Respecto del espejo, el punto O»’ está a una distancia de 10+20=30 cm.
Aplicamos la ecuación de los espejos:
![]()
Llegamos a una ecuación con dos incógnitas, el radio del espejo y la distancia imagen. Vamos a buscar esa distancia imagen de otra forma. El enunciado nos dice que la imagen final, O»», es virtual, luego estará a la derecha del vértice del espejo. Esa distancia imagen S’E será por tanto positiva. Además, la imagen debe ser 3.375 veces menor que el objeto. Si llamamos y a la altura del objeto, la altura de la imagen será:
![]()
El aumento lateral del sistema será el producto de los aumentos de todos los elementos que lo forman, luego:
![]()
donde S’E será positivo puesto que la imagen es virtual. Además el aumento lateral es la relación entre el tamaño de la imagen y el tamaño del objeto luego:
![]()
Igualamos las dos expresiones que hemos obtenido para β:
![]()
Ya tenemos que la imagen final O»» está situada a la derecha del espejo y a 80 cm de él. Si ahora retomamos la ecuación de los espejos y sustituimos esta distancia:
![]()
El radio del espejo es de 96 cm:
R=96 cm
Además, como este radio es negativo, implica que el espejo es un espejo cóncavo.
ESPEJO CÓNCAVO
El sistema completo, con todas las imágenes intermedias y con el espejo, queda como se muestra en la siguiente figura: