Problema de Movimiento Oscilatorio

Aparece en la convocatoria JUL2000

Un arco de circunferencia (OA) de longitud 50 cm está sujeto a un eje vertical en un punto O. En dicho arco de circunferencia se insertan dos muelles, de masa despreciable, con uno de sus extremos unidos a una masa puntual (m=200 g) también insertada en el arco de circunferencia. Cada muelle tiene uno de sus extremos unido a la masa m; el muelle 1 tiene su segundo extremo unido al punto O, mientras que el muelle 2 tiene su segundo extremo unidos al punto A. Todo el conjunto muelles-masa puede deslizar sin rozamiento sobre el arco de circunferencia OA. Se conoce el valor de la constante del muelle 2, k2=50 N/m y los valores de las longitudes naturales de los dos muelles, l01=15 cm y l02=20 cm. Si se considera que el arco de circunferencia permanece inmóvil:

a) Calcular el valor de la constante del muelle 1, k1, si la posición de equilibrio de la masa está dada por θ=40o

b) Si ahora se provocan oscilaciones en torno a dicha posición de equilibrio, desplazando la masa hasta una posición θ=42o y dejándose libre a continuación, calcular la posición y velocidad lineal de la masa, 10 s después de iniciado el movimiento.

a) k1=36.32 N/m
b) θ=41.875o; v=-1.66 m/s

a) Podemos determinar el radio del arco de circunferencia teniendo en cuenta que el arco es igual al radio por el ángulo:

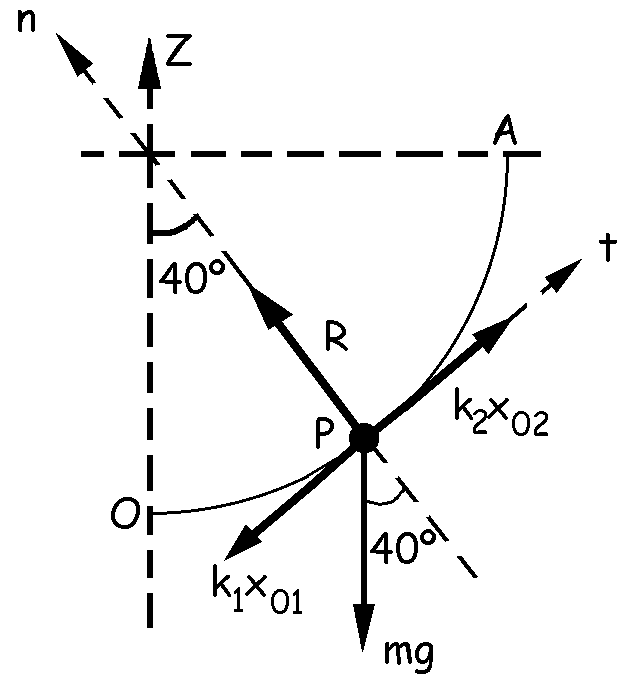Realizamos el diagrama de sólido libre de la masa m. Dada la longitud natural de los resortes, que suman 20+15=35 cm, y la longitud del arco de circunferencia, 50 cm, los dos resortes deben estar estirados. Utilizaremos los ejes marcados en la figura, el eje normal (n) y el tangencial (t). Llamamos además x01 y x02 a las elongaciones en la posición de equilibrio de los resortes 1 y 2 respectivamente. Estas elongaciones pueden calcularse sin más que restar la longitud del arco correspondiente menos la longitud natural de cada resorte:

Planteamos ahora la ecuación de fuerzas en el eje tangencial. Como el sistema está en equilibrio, el sumatorio de fuerzas en esta dirección tiene que ser nulo:

ΣFt=0 ⇒ -k1x01+k2x02-mgsen40=0 ⇒ -0.072k1+50 · 0.0775-0.2 · 9.8sen40=0

k1=36.32 N/m

 

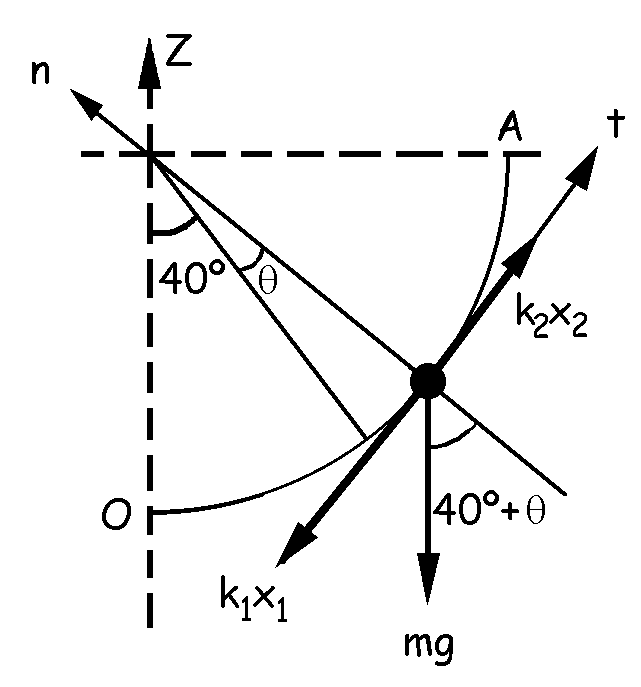b) Ahora desplazamos ligeramente la masa hacia arriba un ángulo θ
y a partir de ahí la dejamos oscilar. La masa ya no está en equilibrio, sino que realizaría un movimiento oscilatorio, y tendría una aceleración. Si desplazamos la masa m hacia arriba, el resorte 1 estará más estirado que en la posición de equilibrio, mientras que el resorte 2 estará menos estirado. El diagrama de sólido libre será el que aparece en la figura. En el caso de los dos resortes, las elongaciones serán las del equilibrio, más o menos el arco comprendido bajo el ángulo θ. Tendremos pues:

x1=x01+Rθ; x2=x02-Rθ

Como el sistema ya no está en equilibrio, el sumatorio de fuerzas será el producto masa por aceleración. En la dirección tangencial (t):

La velocidad de la partícula en coordenadas tangenciales es:

Por tanto la aceleración tangencial es:

Nos queda pues:

Deshacemos los paréntesis y tenemos en cuenta el seno de una suma:

sen(a+b)=senacosb+cosasenb

Sustituyendo:

Como las oscilaciones son muy pequeñas, el ángulo θ es muy pequeño y podemos realizar la aproximación:

senθ » 0

cosθ » 1

Con lo cual nos queda:

Además, del primer apartado sabemos que:

-k1x01+k2x02-mgsen40=0

Luego podemos eliminar estos términos de la ecuación:

Tenemos la ecuación de un movimiento armónico simple, del tipo , de modo que la frecuencia angular será:

La solución del movimiento será del tipo:

θ=θ0cos(ωt+φ0)

La amplitud del movimiento es:

θ0=2º=0.0349 rad

El ángulo de desfase podemos determinarlo a partir de las condiciones iniciales:

t=0 ⇒ θ=θ0 ⇒ θ0=θ0cosφ0 ⇒ cosφ0=1 ⇒ φ0=0

Por tanto la ecuación del movimiento es:

θ=θ0cos(ωt+φ0)=θ0cosωt=0.0349cos(20.77t)

Para t=10 s tendremos:

θ=0.0349cos(20.77t)=0.0349cos(20.77 · 10)=0.0327 rad=1.875º

Por tanto la posición será:

θ=40+1.875=41.875º

θ=41.875º

Para la velocidad tendremos que derivar respecto del tiempo:

Para t=10 s:

Y como la trayectoria es circular:

v=-1.66 m/s