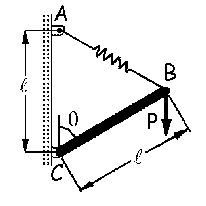
a) θ=83.62o
b) P=10 N
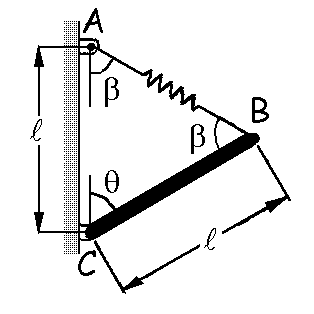 a) Nos centramos en primer lugar en el sistema cuando aún no se ha aplicado la fuerza P. Podemos ver que el triángulo ABC es equilátero (dos de sus lados tienen una longitud de 50 cm) por lo que los ángulos que lo forman serán lo que aparecen en el gráfico. Así:
a) Nos centramos en primer lugar en el sistema cuando aún no se ha aplicado la fuerza P. Podemos ver que el triángulo ABC es equilátero (dos de sus lados tienen una longitud de 50 cm) por lo que los ángulos que lo forman serán lo que aparecen en el gráfico. Así:
β+2θ=180 ⇒ β=180-2θ=180-2 · 60=60º
Por tanto, como los tres ángulos del triángulo son iguales, los tres lados también lo serán, y el lado AB mide también 50 cm. Además, puesto que el miembro BC es un miembro de dos fuerzas (el resorte y la reacción en C) dichas reacciones deben ser iguales, de sentido contrario, y tener la dirección de la recta que une sus puntos de aplicación, es decir, la dirección de la recta BC. Obviamente la reacción del resorte tiene la dirección AB, luego la única solución es que el resorte esté sin deformar y las dos reacciones, la del muelle y la del pasador, sean nulas. Tendremos por tanto que en ausencia de P el resorte está sin deformar y podemos asumir que su longitud natural será 50 cm:
![]()
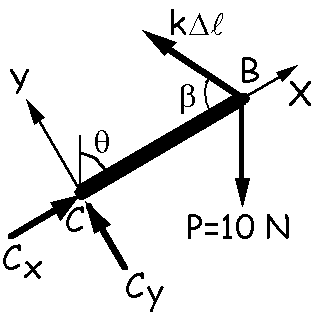 Ahora aplicamos una fuerza P=10 N, con lo cual las reacciones cambian. Trazamos el diagrama de sólido libre del sistema y tendremos lo que aparece en la figura, y utilizaremos el sistema de ejes marcados. Los ángulos θ y β serán diferentes a los vistos cuando no existía P.
Ahora aplicamos una fuerza P=10 N, con lo cual las reacciones cambian. Trazamos el diagrama de sólido libre del sistema y tendremos lo que aparece en la figura, y utilizaremos el sistema de ejes marcados. Los ángulos θ y β serán diferentes a los vistos cuando no existía P.
Aplicando las ecuaciones de la estática, podemos tomar momentos respecto de un eje Z que pase por B:
ΣMZB=0 ⇒ -0.5Cy=0 ⇒ Cy=0
Obtenemos por tanto que la reacción en C sólo tiene componente en X. Esto es lógico, ya que la reacción en C y la resultante del resorte y P (fuerzas aplicadas en B) forman un sistema de dos fuerzas, por lo que ambas deben ser iguales, de sentido contrario y dirección la de la recta que une sus puntos de aplicación, es decir, la dirección del eje X. La ecuación de fuerzas del eje Y nos quedará entonces:
![]()
La elongación del resorte será:
![]()
donde hemos aplicado el teorema del coseno para determinar la longitud ![]() del tramo AB.
del tramo AB.
Además, puesto que el triángulo ABC es isósceles, tendremos que:
θ+2β=180 ⇒ θ=180-2β
Sustituimos esto en la expresión de la elongación:
![]()
Y además tenemos en cuenta que:
![]()
Sustituimos esto en la ecuación de fuerzas en el eje Y tendremos:
![]()
![]()
![]()
![]()
Podemos tener en cuenta la relación trigonométrica:
sen(2β)=2senβcosβ
Y nos queda:
![]()
![]()
Elevamos al cuadrado los dos miembros de la ecuación:
0.5-0.5cos(2β)=0.52+0.252cos2β+2·0.5·0.25cosb
Ahora tenemos en cuenta la relación trigonométrica:
cos(2β)=cos2β-sen2β
Con lo cual:
0.5-0.5cos2β+0.5sen2β=0.25+0.0625cos2β+0.25cosβ
Como:
sen2β+cos2β=1 ⇒ sen2β=1-cos2β
Sustituyendo esto en la ecuación:
![]()
El ángulo β tiene que ser menor de 90º, luego la primera de las soluciones no es válida. Tomando la segunda:
β=48.19º ⇒ θ=180-2β=180-2 · 48.19=83.62º
θ=83.62º
b) Conocidos ya todos los ángulos podemos determinar la elongación del resorte:
![]()
Y la reacción en C sólo tiene componente en X. De la ecuación de fuerzas del eje X:
ΣFX=0 ⇒ Cx-kΔlcosβ-Pcosθ=0 ⇒ Cx=kΔlcosβ+Pcosθ=80 · 0.167cos48.19+10cos83.62=10 N
P=10 N