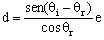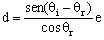
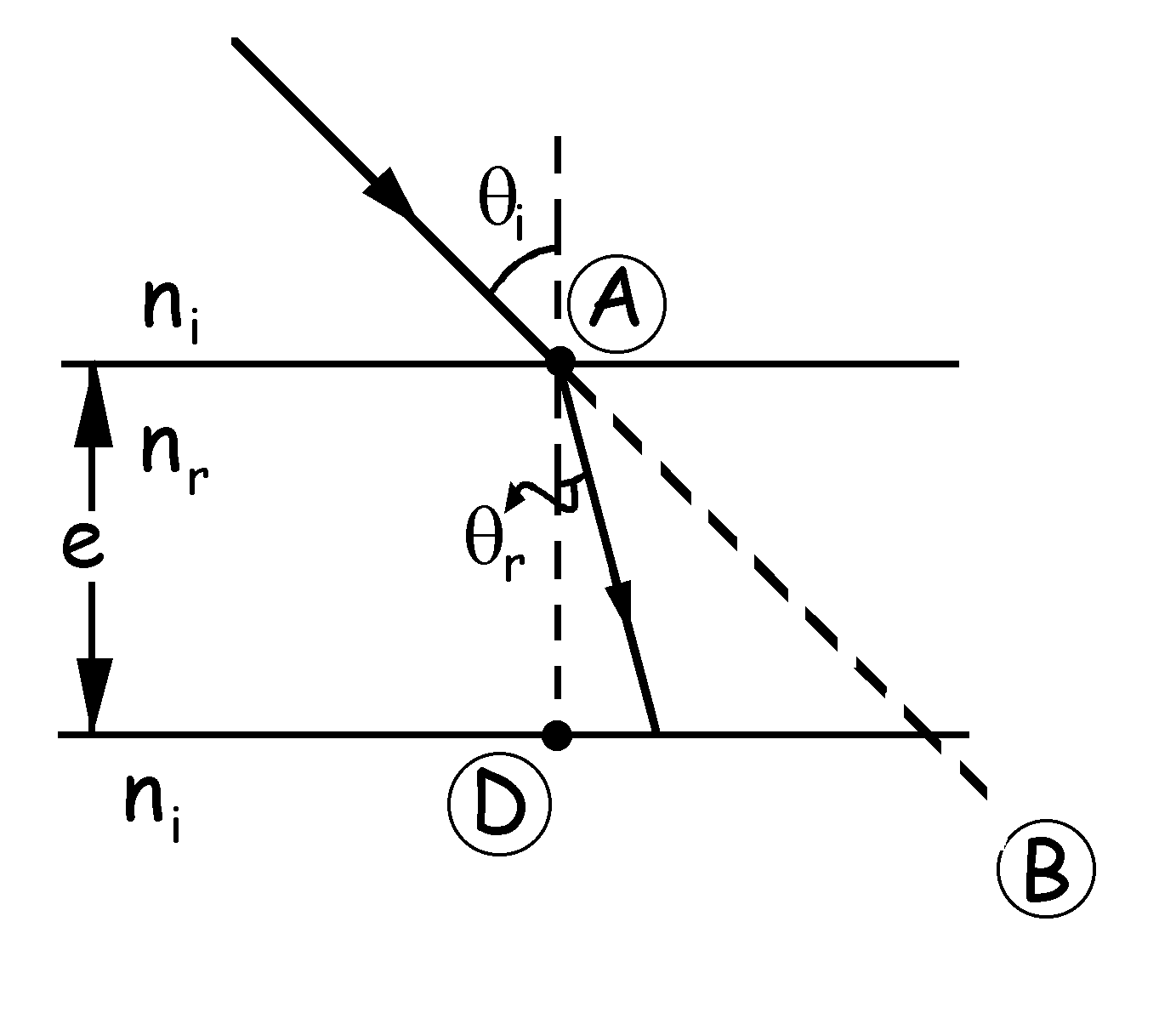
Supongamos un medio limitado por dos caras planas y paralelas, como indica la figura. El espesor de este medio es e. Llamaremos ni al índice de refracción del medio externo y nr al índice de refracción del medio de espesor e. Tendremos el rayo incidente (cuya dirección es la de la recta AB), que llega al punto A. En dicho punto sufre una refracción que deberá verificar la ley de Snell:
nisenθi=nrsenθr
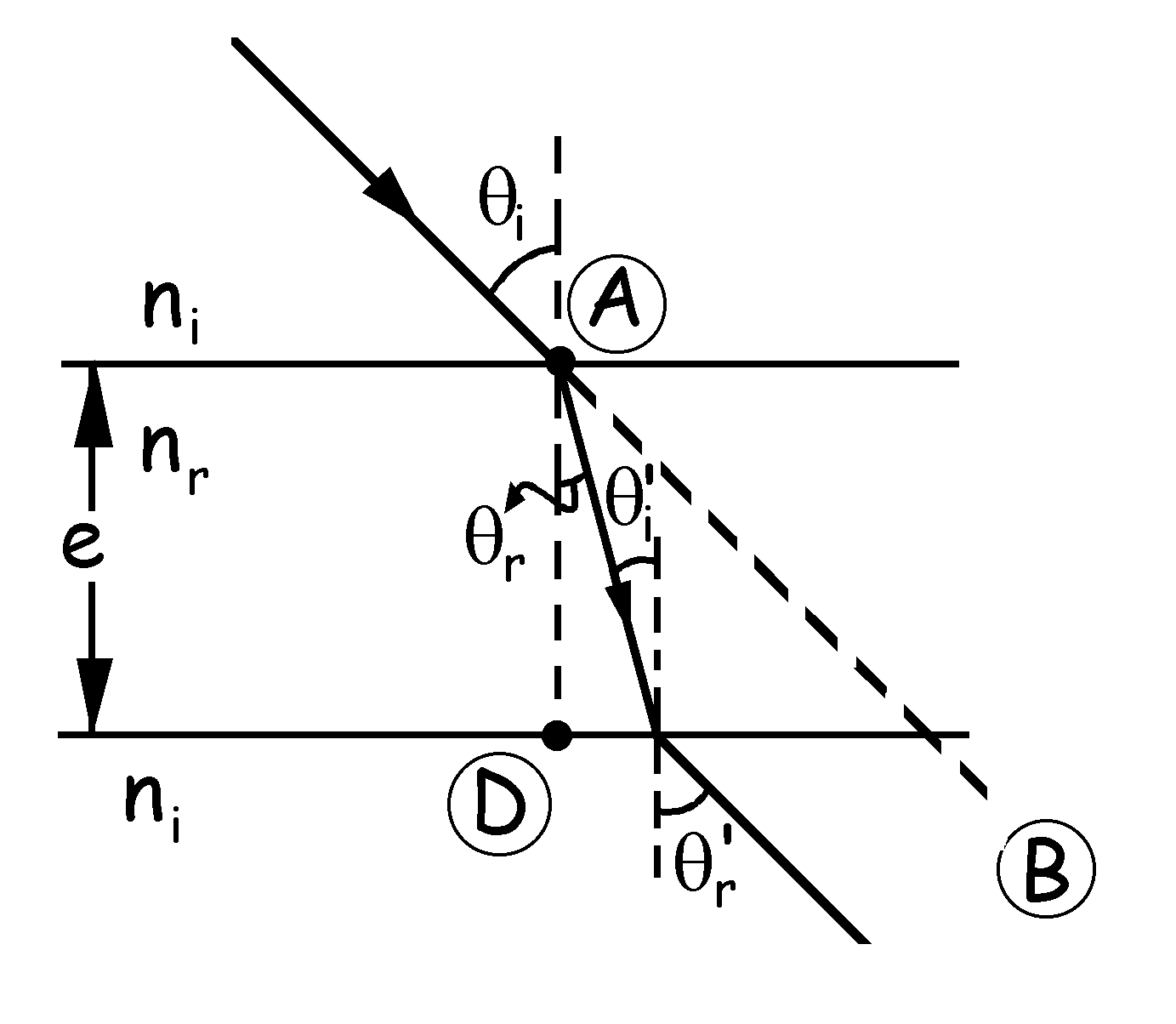
A continuación, el rayo refractado llega el punto C, donde sufre una segunda refracción. El ángulo de incidencia en este caso es θ’i y el ángulo de refracción será θ’r. Se verificará de nuevo la ley de Snell, teniendo en cuenta que ahora el medio de incidencia tiene índice de refracción nr y el de refracción ni:
nrsenθ’i=nisenθ’r
Podemos ver fácilmente en el dibujo que:
θr=θ’i ⇒ senθr=senθ’i ⇒ nrsenθ’i=nisenθ’r ⇒ nrsenθr=nisenθ’r
El primer miembro de esta ecuación es igual al segundo miembro de la primera ecuación, luego podemos igualar los otros dos miembros:
nisenθi=nisenθ’r ⇒ senθi=senθ’r ⇒ θi=θ’r
Luego la dirección del rayo emergente es paralela a la dirección del rayo incidente.
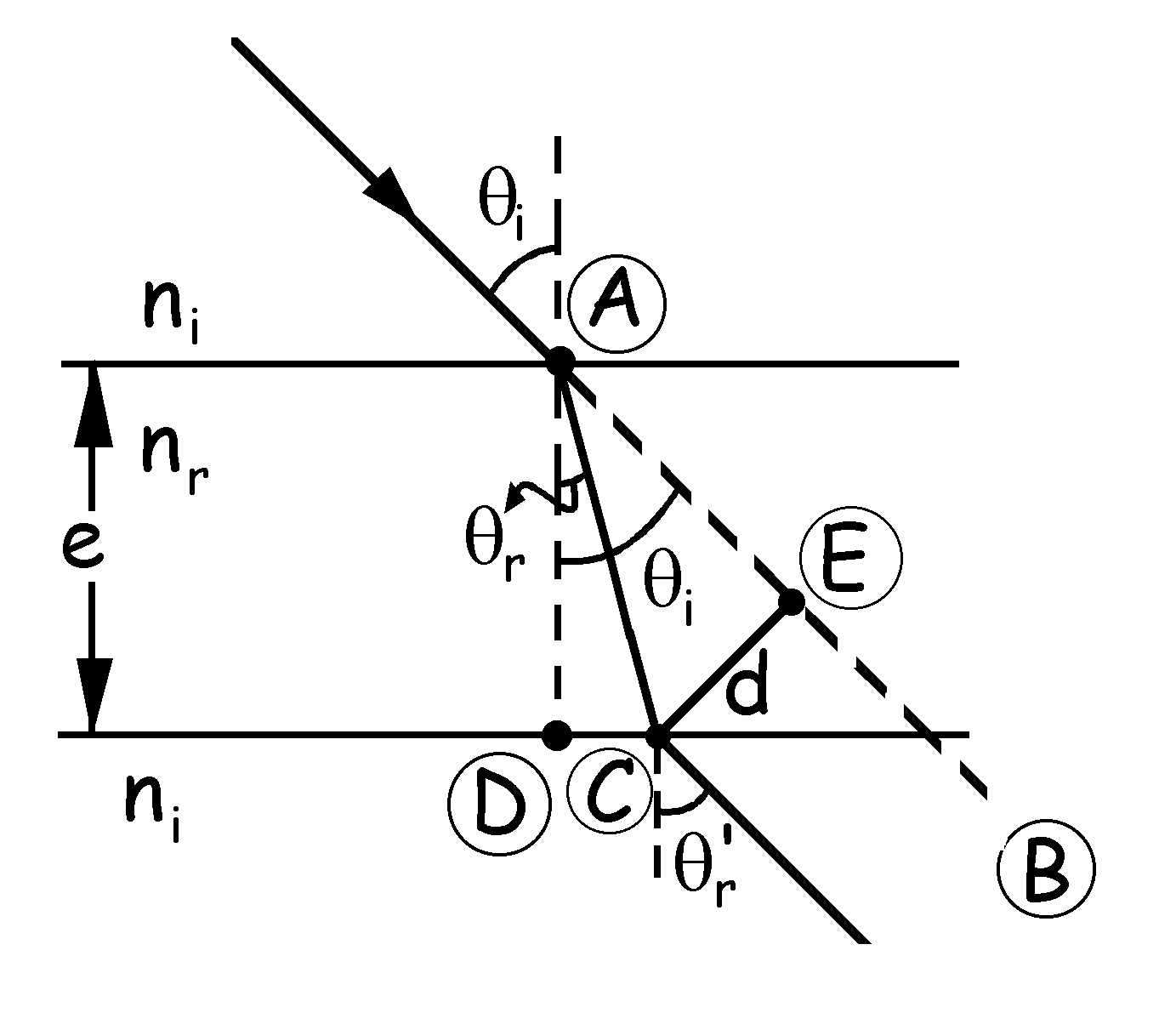
Vamos a ver ahora cuál es el desplazamiento d que sufre el rayo. Tendremos lo que aparece en la figura. El triángulo ACD es un triángulo rectángulo. Para este triángulo:
El triángulo AEC también es rectángulo. Haciendo lo mismo en este triángulo:
Igualando las dos expresiones que tenemos para el lado AC:
