Cuestion de Gravitación

Determinar la distancia mínima a la superficie de la Tierra de un satélite artificial si su distancia máxima es H=900 km, su período de rotación alrededor de la Tierra es T=96 min y sabemos que el semieje mayor de su órbita lunar es R=384400 km, su período alrededor de la Tierra de 27.3 días y el radio terrestre Ro=6370 km.

hmín=302 km

A través de la tercera ley de Kepler, tenemos que el cuadrado de los períodos es directamente proporcional al cubo de los semiejes mayores. Aplicamos esto a la órbita lunar y tendremos:

Si ahora lo aplicamos al caso que nos interesa, es decir, a la órbita que describe el satélite:

Sustituimos la constante k por la expresión que hemos obtenido anteriormente y nos queda:

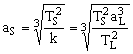
Y conocemos los datos:

TS=96 min=5760 s; aL=384400 km=3.844 · 108 m; TL=27.3 días=2358720 s

Sustituyendo los valores:

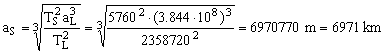
Tenemos como dato también la altura máxima de la órbita, luego podemos determinar el radio máximo de dicha órbita:

H=900 km ⇒ rmáx=H+R0=900+6370=7270 km

Y teniendo en cuenta que:

2aS=rmáx+rmín ⇒ rmín=2aS-rmáx=2 · 6971-7270=6672 km

Y por tanto la altura:

hmín=rmín-R0=6672-6370=302 km

hmín=302 km