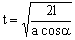aC/V=acosα; N=masenα; 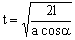
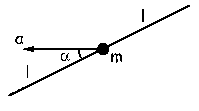
 La varilla se encuentra en un plano horizontal, luego el peso de la cuenta se equilibra con la reacción normal que ejerce la varilla sobre la cuenta en dirección vertical. Dado que no existe fricción, sobre la cuenta actuará sólo, en el plano del movimiento, la reacción de la varilla, que será perpendicular a ella. Como debe verificarse la segunda ley de Newton, ΣF=ma, la aceleración absoluta de la varilla debe tener la misma dirección y sentido que esa reacción normal. Como sólo existe traslación, la aceleración relativa de la cuenta respecto de la varilla será:
La varilla se encuentra en un plano horizontal, luego el peso de la cuenta se equilibra con la reacción normal que ejerce la varilla sobre la cuenta en dirección vertical. Dado que no existe fricción, sobre la cuenta actuará sólo, en el plano del movimiento, la reacción de la varilla, que será perpendicular a ella. Como debe verificarse la segunda ley de Newton, ΣF=ma, la aceleración absoluta de la varilla debe tener la misma dirección y sentido que esa reacción normal. Como sólo existe traslación, la aceleración relativa de la cuenta respecto de la varilla será:
aC/V=aC–aV
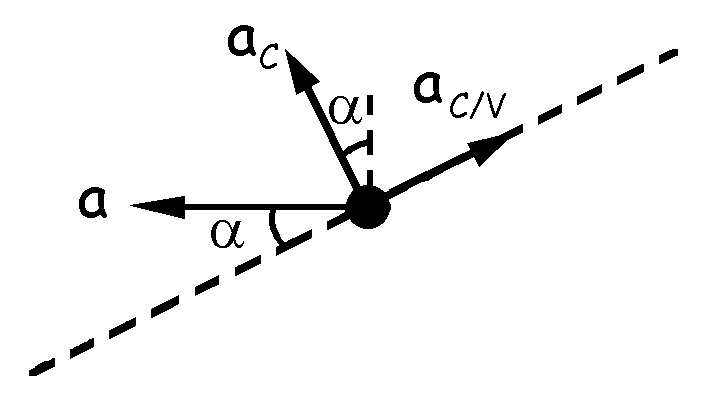 Tomaremos como eje X el de la varilla, y como eje Y el perpendicular a él, es decir, el de la norma. La aceleración de la varilla vale a en la dirección que nos indica el enunciado. La aceleración de la cuenta respecto de la varilla tendrá la dirección de la varilla, luego entonces:
Tomaremos como eje X el de la varilla, y como eje Y el perpendicular a él, es decir, el de la norma. La aceleración de la varilla vale a en la dirección que nos indica el enunciado. La aceleración de la cuenta respecto de la varilla tendrá la dirección de la varilla, luego entonces:
aC/Vi=aCj+acosαi-asenαj
Separando componentes en los dos ejes tendremos:
Eje X: aC/V=acosα
aC/V=acosα
Y del eje Y:
Eje Y: 0=aC-asenα ⇒ aC=asenα
Para determinar la reacción de la varilla sobre la cuenta aplicamos la segunda ley de Newton en el diagrama de fuerzas y tendremos:
ΣFY=maY ⇒ N=maC=masenα
N=masenα
Hemos obtenido que la aceleración relativa de la cuenta respecto de la varilla es constante, ya que tanto la aceleración a como el ángulo α lo son. Entonces respecto de la varilla el movimiento es rectilíneo uniformemente acelerado, recorriéndose una longitud l. Suponiendo que tanto el espacio como la velocidad inicial son nulas y tomando como origen el centro de la varilla, el tiempo que tarda la cuenta en abandonar la varilla será:
![]()