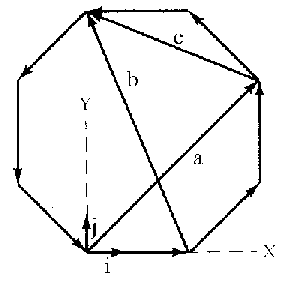
a) v₁=25i; v₂=17.68i+17.68j; v₃=25j; v₄=-17.68i+17.68j; v₅=-25i; v₆=-17.68i-17.68j; v₇=-25j; v₈=17.68i+17.68j.
b) a=60.36 mm; θ_a=45^o; b=62.33 mm; θ_b=157.50^o; c=46.20 mm; θ_c=157.50^o.

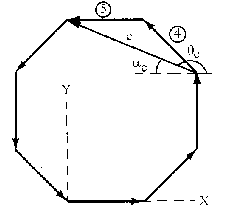
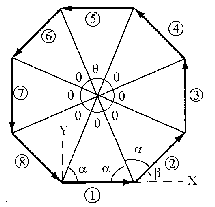Daremos un número a cada vector para que no haya confusiones. En el gráfico podemos ver el número asociado a cada vector. Vamos a determinar además los ángulos que forman cada vector con los ejes. Podemos ver que se forman ocho triángulos iguales. Los ángulos centrales serán:

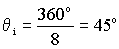
Como los triángulos son todos ellos isósceles, los otros dos ángulos de cada triángulo serán de:

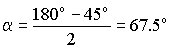
cada uno, lo que hace que el ángulo que forma el vector 2 por ejemplo, con el eje X sea de:

β=180^º-2 · 67.5^o=45^º.

Los otros vectores tienen ángulos análogos. Ahora vamos determinando los ocho vectores:

v₁=25i

v₂=25cos45^oi+25sen45^oj=17.68i+17.68j

v₂=17.68i+17.68j

v₃=25j

v₄=-25cos45^oi+25sen45^oj=-17.68i+17.68j

v₄=-17.68i+17.68j

v₅=-25i

v₆=-25cos45^oi-25sen45^oj=-17.68i-17.68j

v₆=-17.68i-17.68j

v₇=-25j

v₈=25cos45^oi-25sen45^oj=17.68i+17.68j

v₈=17.68i+17.68j

 

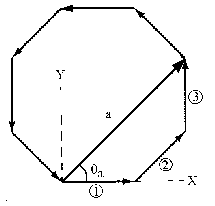El vector a valdrá:

a=v₁+v₂+v₃=25i+17.68i+17.68j+25j=42.68i+42.68j

 

En módulo:

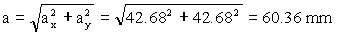
a=60.36 mm

Y el ángulo que forma con el eje X será:

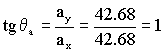
θ_a=45^º

 

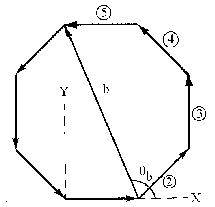Para el vector b haremos lo mismo. Podemos ver en el gráfico que:

b=v₂+v₃+v₄+v₅=

=17.68i+17.68j+25j-17.68i+17.68j-25i=-25i+60.36j

 

En módulo:

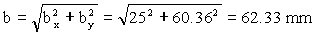
b=62.33 mm

Y el ángulo que forma con el eje X:

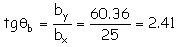
θ_b=157.50^º

 

Y por último, el vector c será:

c=v₄+v₅==-17.68i+17.68j-25i=-42.68i+17.68j

 

En módulo:

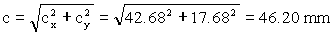
c=46.20 mm

Y el ángulo que forma con el eje X:

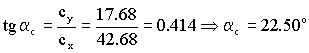
θ_c=180^o-α_c=180^º-22.50^º=157.50^º

θ_c=157.50^º