a) f’=-0.24 m
b) S’=-0.109; β=0.545
c) S’=-0.6 m; β=-1.5
d) S’=1.2 m; β=6
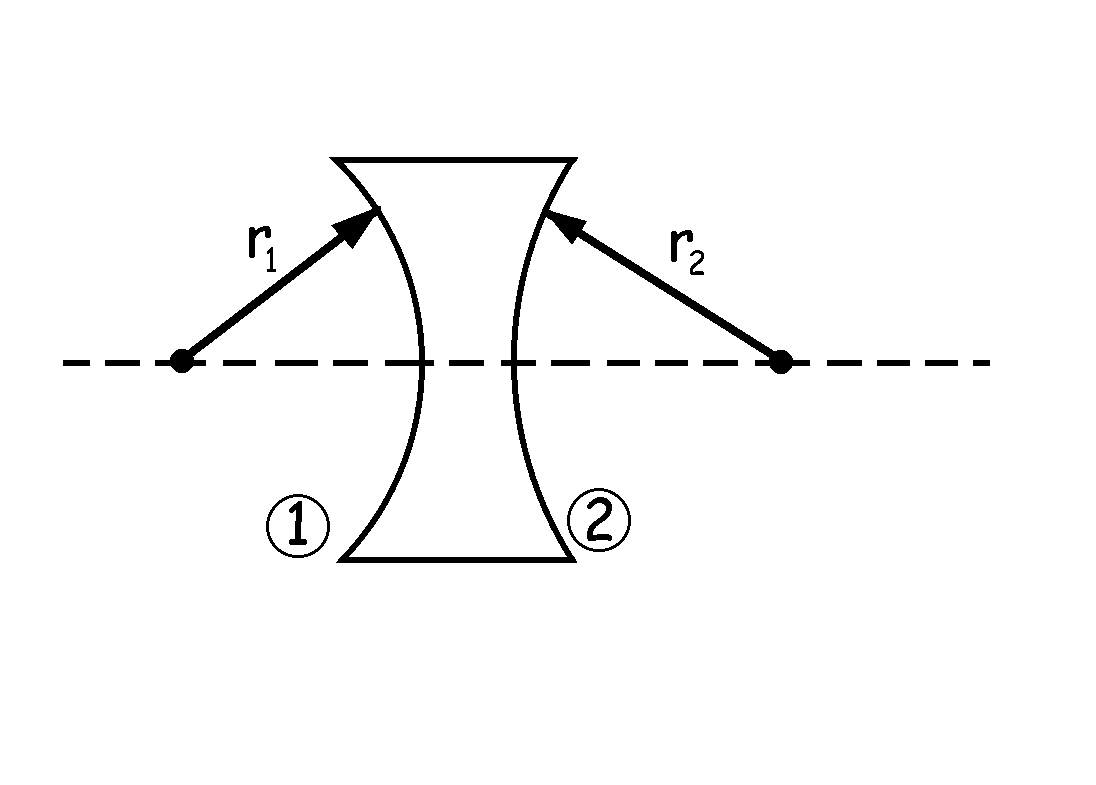a) Tendremos la lente que aparece en la figura. La potencia será:
El radio de la primera cara vale 0.2 m y será negativo, puesto que el centro de curvatura está a la izquierda de la cara, mientras que el radio de la segunda cara es de 0.3 m y es positivo, ya que el centro de curvatura está a la derecha dicha cara. Sustituyendo con los correspondientes signos:
Como la potencia es el inverso de la distancia focal:
f’=-0.24 m
b) El objeto está situado 0.2 m a la izquierda de la lente, luego la distancia objeto será negativa. Aplicando la ecuación de las lentes:
S’=-0.109 m
El aumento lateral será:
β=0.545
c) Si el objeto es virtual estará situado a la derecha de la lente, luego la distancia objeto es positiva. En este caso tendremos:
S’=-0.6 m
Y el aumento lateral:
β=-1.5
d) Y por último tendremos:
S’=1.2 m
Y el aumento lateral:
β=6