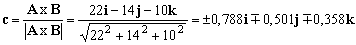a) 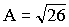 ;
; 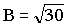
b) A+B=4i+2j+6k
c) A*B=0
d) θ=90o
e) AB=0
f) A X B=22i-14j-10k
g) 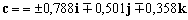
a) Los módulos serán:

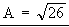
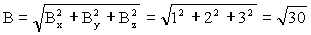
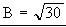
b) Para la suma tendremos:
A+B=3i+4j+k+i-2j+5k=4i+2j+6k
A+B=4i+2j+6k
c) El producto escalar es:
A · B=(3i+4j+k) · (i-2j+5k)=3-8+5=0
A · B=0
d) El módulo del producto escalar es:
A · B=ABcosθ
donde θ es el ángulo que forman los dos vectores. Despejando:
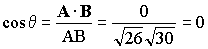
θ=90º
e) Para proyectar un vector sobre una dirección dada se debe multiplicar escalarmente el vector por un unitario en la dirección dada. Esto significa que la proyección de A sobre la dirección de B es igual al producto escalar de A por un vector unitario en la dirección de B. Tendremos entonces:
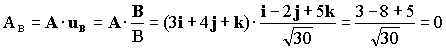
AB=0
f) El producto vectorial es:
A X B=22i-14j-10k
g) Llamaremos C al versor que buscamos. Dicho versor tendrá la forma:
C=Cxi+Cyj+Czk
Como es perpendicular a los vectores A y B los productos escalares por ambos serán nulos, ya que por formar un ángulo de 90º el coseno será nulo. Tendremos por tanto:
A · C=0 ⇒ (3i+4j+k) · (Cxi+Cyj+Czk)=0 ⇒ 3Cx+4Cy+Cz=0
B · C=0 ⇒ (i-2j+5k) · (Cxi+Cyj+Czk)=0 ⇒ Cx-2Cy+5Cz=0
Nos faltaría una ecuación. Tendremos además que por ser un versor su módulo es la unidad, luego:
Cx2+Cy2+Cz2=1
Tenemos un sistema de tres ecuaciones y tres incógnitas:
3Cx+4Cy+Cz=0
Cx-2Cy+5Cz=0
Cx2+Cy2+Cz2=1
De la segunda ecuación:
Cx-2Cy+5Cz=0 V Cx=2Cy-5Cz
Y sustituyendo en la primera:
3Cx+4Cy+Cz=0 ⇒ 3(2Cy-5Cz)+4Cy+Cz=0 ⇒ 6Cy-15Cz+4Cy+Cz=0 ⇒ 10Cy-14Cz=0
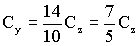
De manera que tendremos que Cx valdrá:
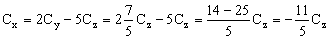
Y sustituyendo todo en la última ecuación:
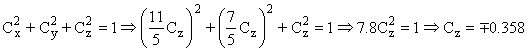
Y las otras dos componentes serán:
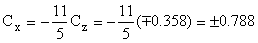
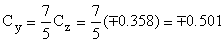
El versor por tanto es:
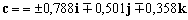
Otra forma de resolver este apartado:
El vector buscado, por ser perpendicular a A y perpendicular a B tendrá la dirección del vector AxB y como es unitario lo calcularemos dividiendo dicho vector por su módulo: