a)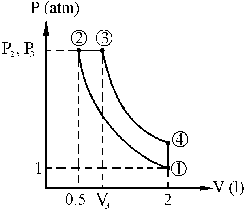 
b) P1=1 atm, V1=2 l, T1=300 K, P2=6.96 atm, V2=0.5 l, T2=522.3 K, P3=6.96 atm, V3=1.5 l, T3=1566.99 K, P4=4.65 atm, V4=2 l, T4=1395 K
c) ΔQ41=-445.12 cal
d) η=0.249
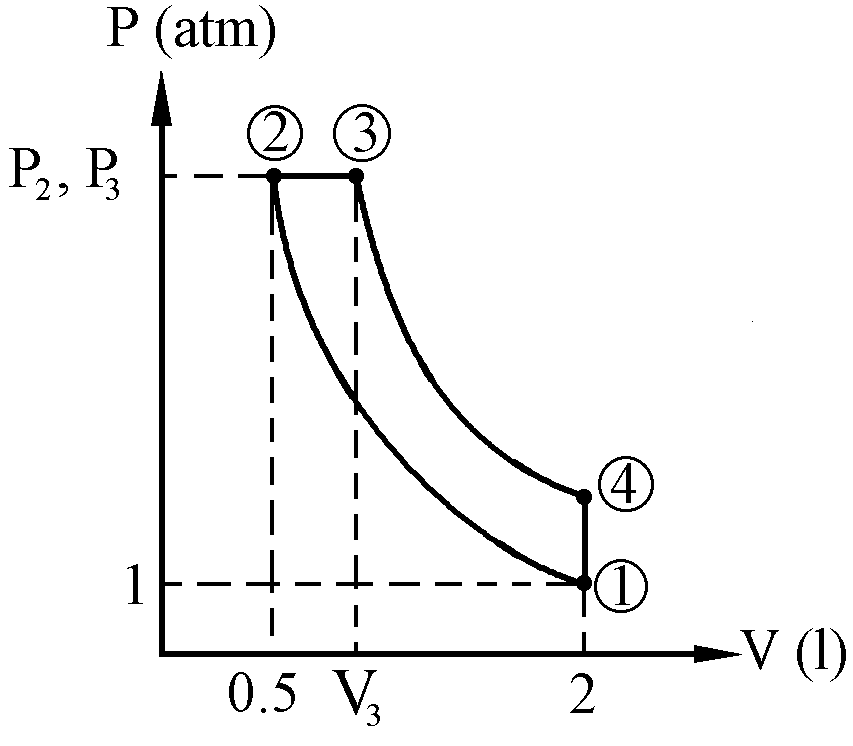a) Vamos a dibujar el ciclo en un diagrama P-V. Colocamos en primer lugar el punto 1 al azar. A continuación tenemos una compresión adiabática, que vendrá representada por una línea curva. Por ser compresión tendremos que disminuirá el volumen y aumentará la presión, pasando así al punto 2. Después se produce un calentamiento a presión constante, lo que implica que aumentará el volumen. Dicho cambio vendrá representado por una línea horizontal paralela al eje X, ya que tenemos que la presión es constante. Llegamos así al punto 3.Tenemos luego una expansión adiabática, es decir, disminuye la presión y aumenta el volumen, hasta tener el mismo volumen que al principio. Los puntos 3 y 4 estarán por tanto unidos por una curva, que representa la transformación adiabática, y además el punto 4 tiene que estar encima del 1, ya que tienen el mismo volumen. Por último se pasa del punto 4 al 1, obviamente a través de una transformación isócora (volumen constante). El ciclo queda pues como aparece en la figura.
b) Conocemos todos los parámetros del estado 1:
P1=1 atm
V1=2 l
T1=300 K
En el estado 2 sabemos el volumen, ya que nos dicen que se reduce a la cuarta parte:
V2=0.5 l
El paso de 1 a 2 es una transformación adiabática, por lo que debe cumplirse que:
P2=6.96 atm
Además el número de moles permanece constante, por lo que teniendo en cuenta la ecuación de los gases perfectos:
T2=522.3 K
El paso del estado 2 al estado 3 se realiza a presión constante luego:
P3=P2=6.96 atm
P3=6.96 atm
Sabemos también que el volumen en el estado 3 es de 1.5 l:
V3=1.5 l
Y podemos determinar la temperatura en este estado teniendo en cuenta que el número de moles permanece constante:
T3=1566.99 K
Por último, en el estado 4 el volumen es el mismo que el inicial:
V4=V1=2 l
V4=2 l
Además del estado 3 al 4 se pasa mediante una transformación adiabática, luego:
P4=4.65 atm
Y la temperatura la determinamos como en los otros casos:
T4=1395 K
c) La transformación del estado 4 al estado 1 es isócora (V=cte) por lo que la variación de trabajo es nula:
ΔW41=0
La variación de energía interna será:
ΔU41=nCV(T1-T4)
El número de moles podemos calcularlo mediante las condiciones en cualquiera de los estados:
Y para el calor específico a volumen constante tendremos en cuenta que conocemos la constante adiabática del gas:
Además, por tratarse de un gas ideal:
Por tanto tendremos:
ΔU41=nCV(T1-T4)=0.0813 · 5(300-1395)=-445.12 cal
A través del primer principio de la Termodinámica:
ΔU41=ΔQ41-ΔW41 ⇒ ΔQ41=ΔU41+ΔW41=ΔU41=-445.12 cal
ΔQ41=-445.12 cal
d) El rendimiento del ciclo es el cociente entre el trabajo y el calor cedido:
Vamos a determinar cada uno de los términos que aparecen. La transformación 1—
2 es adiabática luego el trabajo será:
Por ser una transformación adiabática la variación de calor es nula:
ΔQ12=0
La transformación 2—3 es a presión constante. La variación de trabajo en este caso es:
ΔW23=P2(V3-V2)=6.96(1.5-0.5)=6.96 atml=168.71 cal
Y el enunciado nos dice que en esta transformación se emplean 594.5 cal luego:
ΔQ23=594.5 cal
La transformación 3—4 es adiabática, por lo que el trabajo será:
Y por ser una transformación adiabática la variación de calor es nula:
ΔQ34=0
Para la transformación 4—1 tenemos los cálculos realizados en el apartado c):
ΔW41=0; ΔQ41=-445.12 cal
En el rendimiento del ciclo aparecerán en el numerador todos los trabajos y en el denominador los calores cedidos, es decir, aquéllos que tienen signo positivo:
η=0.249