Problema de Movimiento Ondulatorio

Aparece en la convocatoria JUN2000

Se pretende fabricar una cuerda cilíndrica para una guitarra con 5 g de un acero de densidad 7800 kg/m3 y una resistencia a la rotura de 7·108 N/m2. Calcular: a) la longitud y radio de la cuerda más larga y delgada que pueda someterse a una tensión de 800 N sin romperse; b) la frecuencia fundamental máxima que podría tener esa cuerda; c) supongamos un murciélago que vuela a una velocidad v=5 m/s emite esa misma frecuencia multiplicada por 100. Si la frecuencia que oye el murciélago del sonido reflejado en un insecto es de 28 kHz, ¿el insecto se está alejando o acercando al murciélago? Razona la respuesta. d) Si las direcciones de vuelo de ambos están sobre la línea que une sus posiciones, ¿cuál es la velocidad del insecto?
Velocidad del sonido en las condiciones del problema: v=340 m/s.

a) rmín=0.603 mm; lmáx=0.561 m
b) ν=267.02 Hz
c) El insecto se acerca al murécilago
d) vI=3.08 m/s; vI=13.08 m/s

a) El esfuerzo es el cociente entre la fuerza y la sección. Teniendo en cuenta que la sección de la cuerda es circular:

Si queremos que la cuerda sea lo más delgada posible, es decir, que el radio sea lo más pequeño posible, el esfuerzo será el máximo, y el máximo esfuerzo que puede soportar la cuerda es el de rotura. Por tanto:

rmín=0.603 mm

La longitud de la cuerda podemos obtenerla teniendo en cuenta que la densidad de la misma es masa por unidad de volumen, y que el volumen de la cuerda será el de un cilindro:

Ahora si buscamos la máxima longitud de la cuerda tendremos que el radio debe ser mínimo. Entonces:

lmáx=0.561 m

b) Para que en la cuerda se produjesen ondas estacionarias debería cumplirse que su longitud fuese un número entero de semilongitudes de onda:

Para la frecuencia fundamental:

Como las ondas son transversales:

siendo µ la densidad lineal de la cuerda, es decir, masa por unidad de longitud. Además, puesto que nos piden la frecuencia máxima, será la correspondiente a esa tensión:

ν=267.02 Hz

 

c) Ahora tenemos un problema de efecto Doppler, donde la frecuencia emitida es 26702 Hz y la percibida 28000 Hz. Además existe un problema de reflexión. El murciélago emite una frecuencia ν que el insecto percibe como ν’; a continuación, el sonido se refleja en el insecto, de modo que es como si éste emitiese una frecuencia ν’ y el murciélago percibe ν», conociéndose ν=26702 Hz y ν»=28000 Hz. Llamaremos vI y vM a las proyecciones, sobre la recta que une a ambos, de sus respectivas velocidades, ya que son estas proyecciones las que nos interesan en efecto Doppler. En principio el murciélago será la fuente, que emite una frecuencia ν y el insecto será el observador, que percibe una frecuencia ν’. Por el efecto Doppler tendremos:

En principio, el medio estará en reposo luego:

Se considera positivo el sentido que va de la fuente al observador. Supongamos que las dos velocidades tienen este sentido (luego veremos cuál es el que tienen que tener para que se cumplan las condiciones del problema). Nos quedará la ecuación:

A continuación el sonido se refleja en el insecto, por lo que podemos operar como si el insecto fuese la fuente que emite un sonido de frecuencia ν’ y el murciélago fuese el observador que percibe una frecuencia ν». Como el sentido positivo es el que va de la fuente al observador, ahora habrá cambiado, luego las dos velocidades (la del murciélago y la del insecto) serán negativas. Nos quedará:

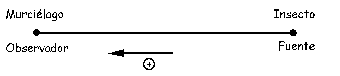
Como ν»>ν su cociente será mayor que la unidad. Podemos tener ahora cuatro casos posibles. El primero de ellos es el que acabamos de suponer, que es que tanto murciélago como insecto se muevan hacia la derecha. Tendremos por tanto la ecuación que se muestra. Vemos que este caso es imposible, ya que y el producto de dos números menores que la unidad no nos puede dar un número mayor que la unidad.

Puede ocurrir también que los dos animales se muevan hacia la izquierda, de modo que sus velocidades tendría los signos al contrario y nos quedaría la expresión:

Este caso sí sería posible, puesto que , y el producto de dos números mayores que la unidad sí daría un número mayor que la unidad. Tendríamos lo que aparece en la figura, donde vemos que el insecto se acercaría al murciélago.

En tercer lugar puede ser que el murciélago se mueva hacia la derecha y el insecto hacia la izquierda. Tendríamos que cambiarían los signos correspondientes al insecto y nos quedaría:

Ahora tendremos que , por lo que el producto será mayor que la unidad dependiendo de cuál de estos factores es mayor. Sabemos que la velocidad del murciélago es de 5 m/s luego nos quedará:

Vemos que el cociente debe ser mayor que la unidad, luego sí puede verificarse esa igualdad, ya que . Por tanto este caso también es posible. El murciélago se mueve hacia la derecha y el insecto hacia la izquierda, tal como aparece en la figura. Así, tenemos que en este caso también el insecto se acerca al murciélago.

Por último podría ocurrir que el murciélago se moviese hacia la izquierda y el insecto hacia la derecha. Respecto al primer caso tendríamos que cambiar los signos correspondientes a la velocidad del murciélago, y nos quedaría:

De nuevo ahora tenemos que luego el producto de los dos factores será mayor que la unidad dependiendo de cuál de los factores es mayor. Si sustituimos los datos conocidos: