a) ε=0.368
b) h_p=408.33 km
c) v_p=8985.55 m/s; v_A=4155.81 m/s
d) T=11019.37 s

a) El radio en el punto que nos dan es:

r=h+R=550+6370=6920 km

Ahora podemos determinar la energía total de la órbita, ya que conocemos velocidad y radio en un mismo punto:

Tenemos que la energía total es negativa luego la órbita tiene que ser cerrada (elipse o circunferencia). Partiremos de que se trata de una elipse, y en el caso de que sea una circunferencia obtendremos que las distancias máxima y mínima son iguales. Podemos pues determinar el semieje mayor de la elipse:

Para obtener la excentricidad de la órbita necesitamos las distancias máxima y mínima (en el apogeo y en el perigeo), ya que la excentricidad vale:

Nos centramos en el perigeo (punto más próximo a la Tierra). La energía total y el momento angular deben permanecer constantes. La ecuación del momento angular es:

L=rmvsenφ

siendo φ el ángulo que forma la velocidad con el radio vector. Como este momento angular es constante:

En el perigeo la velocidad es perpendicular al radio vector, luego:

La otra constante que debe conservarse es la energía total. Si seguimos en el perigeo:

Sustituimos v_P por la expresión que habíamos obtenido para ella a partir del momento angular:

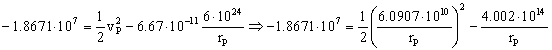
Resolvemos esta ecuación de segundo grado:

Obviamente, si se trata del perigeo, distancia de máximo acercamiento a la Tierra, tiene que ser menor de 6920 km, distancia de la cual se parte. Por ello, debemos desechar la primera solución y quedarnos con la segunda:

r_P=6778.33 km

A partir del eje mayor podemos determinar la distancia en el apogeo:

2a=r_A+r_P ⇒ r_A=2a-r_P=2·10717.09-6778.33=14655.85 km

Esta solución es la otra que habíamos obtenido en la ecuación de segundo grado, lo que es lógico, ya que el apogeo cumple las dos mismas condiciones que hemos aplicado en el perigeo. La excentricidad de la cónica (que ya podemos decir que es una elipse) es:

ε=0.368

 

b) El radio en el perigeo es:

r_P=6778.33 km

Por tanto la altura será:

h_P=r_P-R=6778.33-6370=408.33 km

h_P=408.33 km

 

c) La velocidad del cohete en el perigeo es, sin más que sustituir en la expresión que obteníamos para el momento angular:

v_P=8985.55 m/s

Y para el perigeo podemos aplicar la conservación del momento angular; el momento angular será el mismo en el apogeo y en el perigeo:

L_A=L_P ⇒ r_Pmv_Psenφ_P=r_Amv_Asenφ_A

siendo φ_P y φ_A el ángulo que en cada uno de estos puntos forman el radio vector y la velocidad. En el apogeo y en el perigeo el radio vector es perpendicular a la velocidad, por lo que:

v_A=4155.81 m/s

 

d) Por último, el período de la órbita será:

T=11019.37 s