Problema de Interferencias

Aparece en la convocatoria SEP2000

Dos focos sonoros accionados en fase por un mismo amplificador están en un plano XY en las posiciones (0, 1) y (0, -1) m. En un punto del plano muy alejado de los focos sonoros se oye una interferencia constructiva a un ángulo de 0.140 rad respecto al eje X y la siguiente se escucha a 0.283 rad respecto a dicho eje. a) ¿Cuál es la longitud de onda de las ondas sonoras procedentes de los focos? b) ¿Cuál es la frecuencia? c) ¿A qué otros ángulos se escucha interferencia constructiva? Determínalos todos. d) ¿Cuál es el ángulo menor para el que se cancelarán completamente las ondas sonoras? Velocidad del sonido: v=340 m/s.

a) λ=0.279 m
b) ν=1216.94 s-1
c) θ3=0.432 rad; θ4=0.592 rad; θ5=0.772 rad; θ6=0.992 rad; θ7=1.354 rad
d) θ=0.070 rad

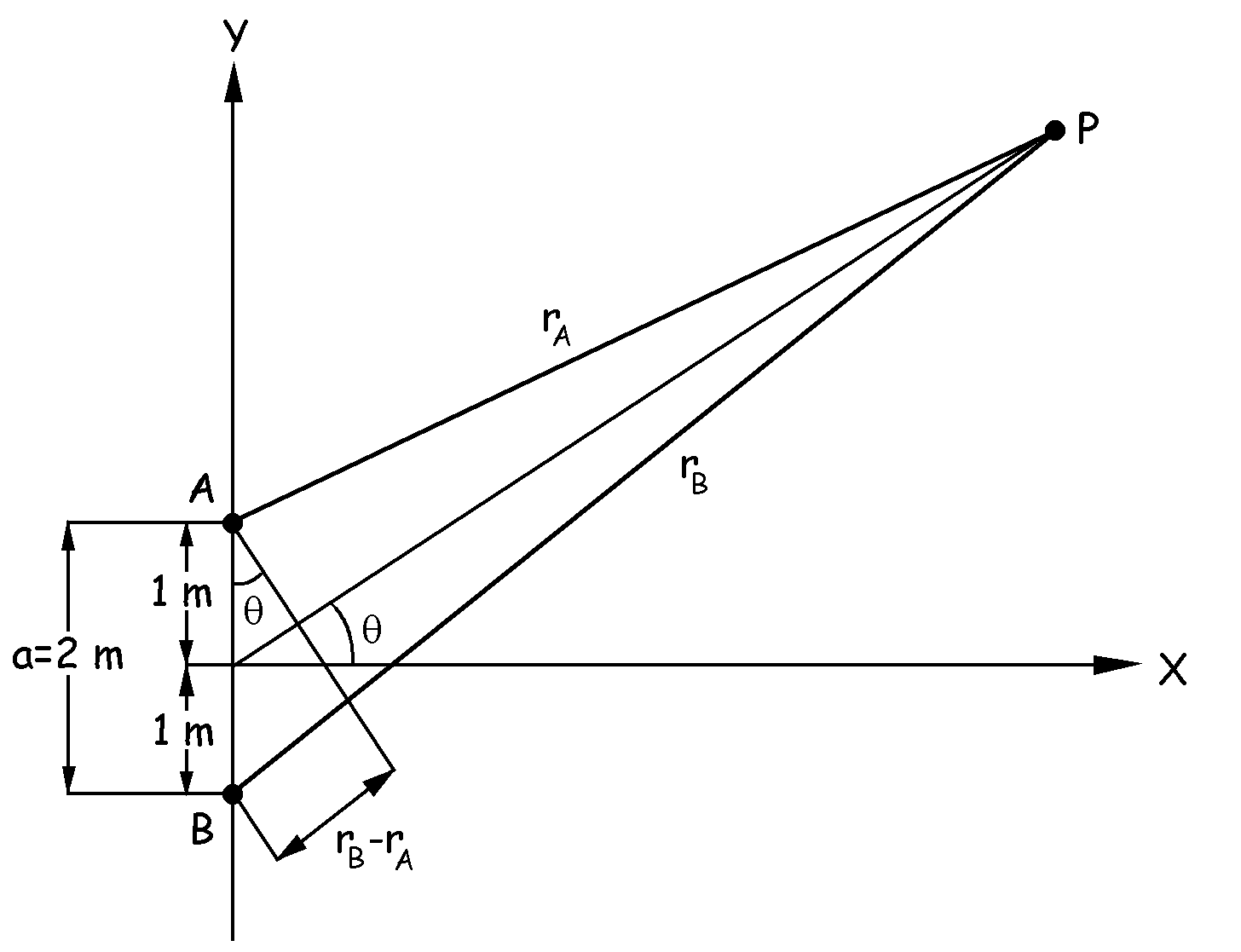a) Tendremos lo que aparece en la figura, es decir, dos fuentes sincrónicas A y B separadas por una distancia a=2 m. Muy lejos de ellas, en el punto P, se produce la interferencia. Puesto que el punto P está muy alejado de A y B podemos suponer que los dos ángulos marcados en el gráfico como θ son iguales, ya que están comprendidos entre rectas prácticamente perpendiculares. Para que se produzca una interferencia constructiva, el desfase entre los dos rayos procedentes de A y B debe ser un número par de veces π:

δ=Nπ

siendo N un número par. En nuestro caso el desfase está dado porque los dos rayos recorren caminos diferentes. Si llamamos θ1 al ángulo a que se produce el primer máximo tendremos:

Tenemos dos máximos consecutivos, luego si en este, que se produce a ángulo θ1, ponemos N, en el siguiente, que se producirá a un ángulo mayor θ2, tendremos que poner N+2, ya que dos números pares consecutivos se diferencian en dos unidades. Por tanto nos quedaría, con el mismo razonamiento:

Restamos las dos expresiones miembro a miembro:

Sustituyendo los datos del problema:

λ=a(senθ2-senθ1)=2(sen0.283-sen0.140)=0.279 m

λ=0.279 m

 

b) Para la frecuencia tendremos:

ν=1216.94 s-1

 

c) La condición de máximo que hemos obtenido es:

siendo N un número par. Vamos a ver primer el orden de los máximos de 0.140 y 0.283 rad. El primero será:

Tenemos por tanto, que excepto para el máximo central que se producirá a ángulo 0, los dos máximos de los que habla el problema son los correspondientes a N=2 y N=4, así que nos quedará a partir de N=6. Tendremos pues:

Por tanto el tercer máximo será:

θ3=0.432 rad

Tendremos ahora que ir dando valores a N teniendo en cuenta que deben ser números pares consecutivos:

θ4=0.592 rad

 

θ5=0.772 rad

 

θ6=0.992 rad

 

θ7=1.354 rad

 

Este ya no nos valdría puesto que el seno del ángulo no puede ser mayor que la unidad.

d) En cuanto a la condición de mínimo, tendremos que el desfase entre los dos rayos tiene que ser igual a un número impar de veces π:

δ=N’π

siendo N’ un número impar. En nuestro caso el desfase está dado porque los dos rayos recorren caminos diferentes:

Vemos que a medida que aumenta N’ aumentará el senθ y por tanto θ, luego el menor ángulo a que se producen mínimos corresponderá al menor valor de N’. Puesto que N’ debe ser un número impar, el menor valor del mismo será 1:

θ=0.070 rad