w_Sur=700 N; w_Ecuador=697.59 N

Como la Tierra gira sobre su eje, no es precisamente un marco de referencia inercial. Por esta razón el peso aparente de un cuerpo en la Tierra no es exactamente igual a la atracción gravitatoria terrestre, a la que llamaremos peso verdadero w₀ del cuerpo. Tendremos una balanza de resorte. La balanza aplica una fuerza de tensión F al cuerpo, y la lectura de la balanza es la magnitud F de dicha fuerza. Si no somos conscientes de la rotación de la Tierra, pensaremos que la lectura de la báscula es igual al peso del cuerpo ya que pensaremos que la balanza está en equilibrio. Pensaremos entonces que la tensión F se opone a una fuerza igual y opuesta w a la que llamaremos peso aparente. Pero si los cuerpos giran junto con la Tierra, no están en equilibrio.

Supongamos que la Tierra es esférica. El peso verdadero tendrá una magnitud:

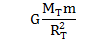donde M_T y R_T son la masa y el radio de la Tierra. Este valor es el mismo para todos los puntos sobre la superficie terrestre. Si tomamos el centro de la Tierra como origen de un sistema de coordenadas inercial, el cuerpo en los polos Norte y Sur está realmente en equilibrio en un sistema inercial, y la lectura de la balanza de resorte es igual al peso verdadero del cuerpo. Por tanto en el polo Sur la balanza indica lo mismo que en el polo Norte, es decir, 700 N:

w_Sur=700 N

Por ser este peso el peso real podemos determinar la masa del cuerpo:

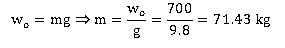
En cambio, en el Ecuador el cuerpo se mueve en un círculo de radio R_T con velocidad v, y tendremos una aceleración normal hacia dentro del círculo. Entonces se verificará:

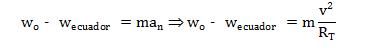
El peso aparente por tanto, que será la lectura de la balanza, será:

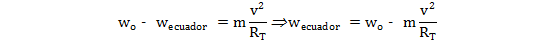
Para determinar la velocidad v podemos tener en cuenta que el movimiento es circular y uniforme:

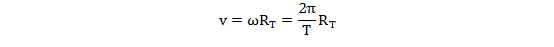
siendo el período el de la rotación de la Tierra:

T=24 h=86400 s

Sustituyendo todo:

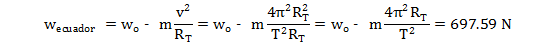
w_Ecuador=697.59 N