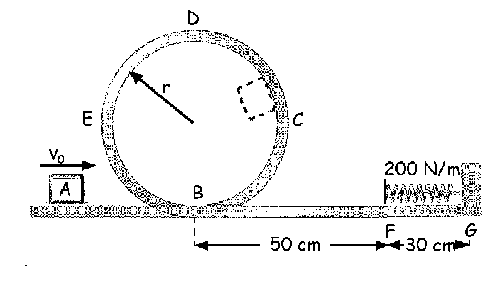
a) v0=3.83 m/s
b) F=7.35 N
c) Δl=12.07 cm
a) Vamos a resolver el problema utilizando para todas las magnitudes unidades del Sistema Internacional.
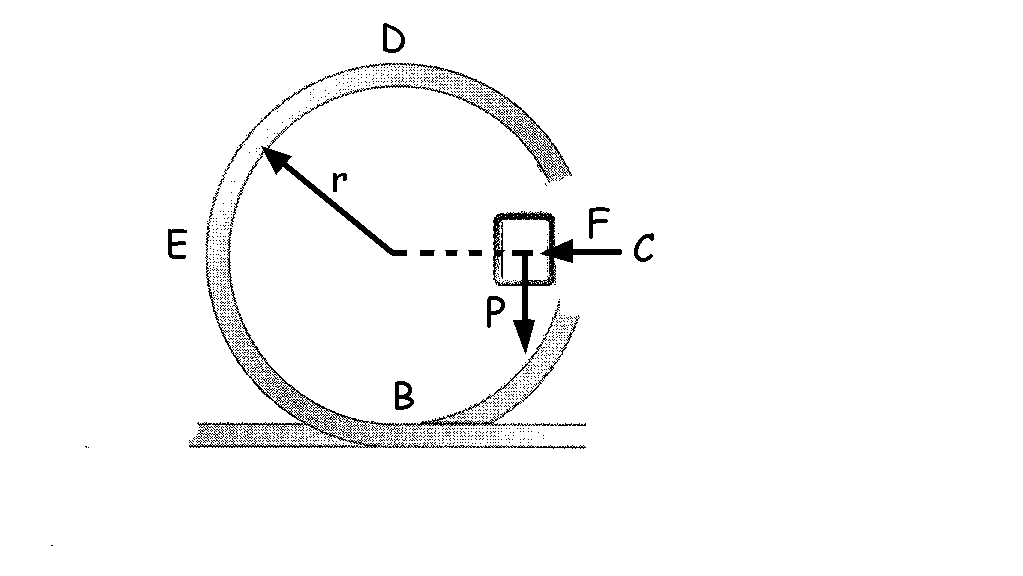
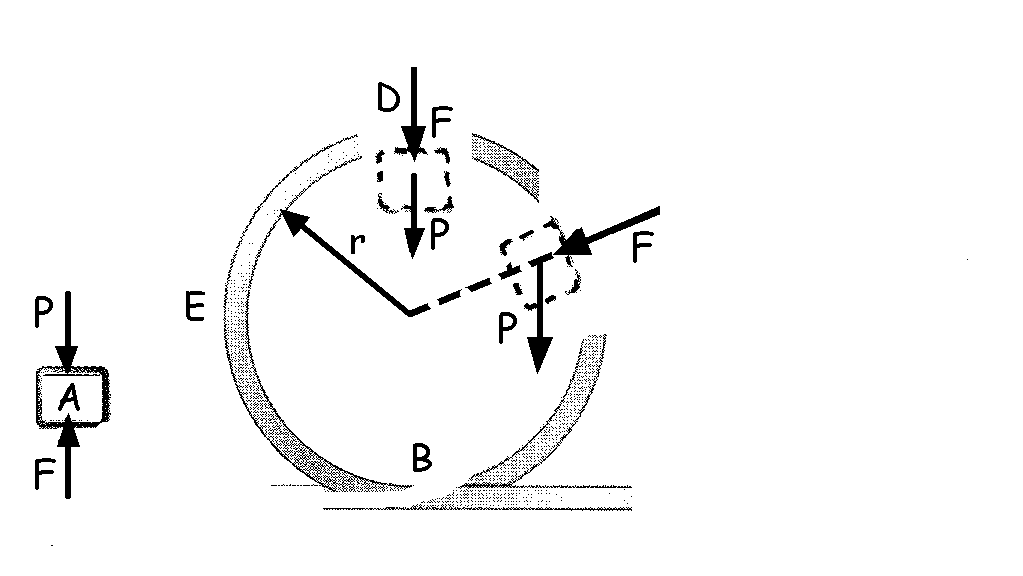 Como el bucle es liso podemos considerar despreciable la fuerza de rozamiento. Al aislar el bloque y hacer el diagrama de sólido libre correspondiente al mismo en distintas posiciones tenemos lo que aparece en la figura. Las fuerzas que actúan sobre el bloque son la fuerza de atracción gravitatoria, que es igual al peso del bloque (P), y la acción que ejerce el raíl del bucle (F). Ésta fuerza F tiene en todo instante la dirección del radio de curvatura, es decir, perpendicular al desplazamiento del bloque, por lo que el trabajo que realiza es nulo.
Como el bucle es liso podemos considerar despreciable la fuerza de rozamiento. Al aislar el bloque y hacer el diagrama de sólido libre correspondiente al mismo en distintas posiciones tenemos lo que aparece en la figura. Las fuerzas que actúan sobre el bloque son la fuerza de atracción gravitatoria, que es igual al peso del bloque (P), y la acción que ejerce el raíl del bucle (F). Ésta fuerza F tiene en todo instante la dirección del radio de curvatura, es decir, perpendicular al desplazamiento del bloque, por lo que el trabajo que realiza es nulo.
La única fuerza que realiza trabajo en el desplazamiento del bloque es por tanto el peso, y como es una fuerza conservativa el trabajo realizado al desplazarse de un punto a otro es igual a la diferencia de energía potencial entre dichos puntos. Por otra parte el trabajo de esa fuerza es el responsable de la variación de energía cinética que experimenta el bloque. Podemos expresarlo como:
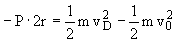
El peso es:
P=mg
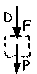 Para determinar la velocidad v0 mínima necesaria para que recorra el bucle hemos de determinar previamente la velocidad mínima con que debe llegar el bloque a D. Si aislamos el bloque en esa posición y tenemos el diagrama de sólido libre que se muestra. Aplicando la segunda ley de Newton:
Para determinar la velocidad v0 mínima necesaria para que recorra el bucle hemos de determinar previamente la velocidad mínima con que debe llegar el bloque a D. Si aislamos el bloque en esa posición y tenemos el diagrama de sólido libre que se muestra. Aplicando la segunda ley de Newton:
ΣF=m·a
y teniendo en cuenta que las fuerzas tienen la misma dirección y sentido (dirección la del radio de curvatura y sentido hacia el centro) podemos poner:

con valores para F≥0 si el bloque se mantiene en contacto con el raíl. El mínimo valor de vD para que se mantenga en contacto con el raíl es el correspondiente a F=0:
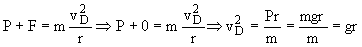
Sustituimos este valor de vD en la ecuación de la energía:
![]()
![]()
vO=3.83 m/s
 b) Para calcular la fuerza que el raíl ejerce sobre el bloque en el punto C aislamos al bloque en ese punto. Aplicamos las mismas leyes que en el apartado anterior. Aquí tenemos:
b) Para calcular la fuerza que el raíl ejerce sobre el bloque en el punto C aislamos al bloque en ese punto. Aplicamos las mismas leyes que en el apartado anterior. Aquí tenemos:
ΣF=ma
En dirección tangencial:
P=matangencial
Y en la dirección normal:
![]()
Para determinar la velocidad en el punto C utilizamos la ecuación correspondiente a la energía:
![]()
Y sustituyendo en la ecuación de fuerzas:
![]()
F=7.35 N
c) La energía que tiene el bloque cuando llega al punto B después de haber recorrido el bucle es la misma que tenia inicialmente:
![]()
Pero cuando el bloque sigue moviéndose por el tramo horizontal BG, que es rugoso, se disipa energía debido al rozamiento.
La energía disipada desde el punto B al F que es donde empieza el muelle podemos calcularla por:
W=FRozamientod
siendo d la distancia BF, y:
FRozamiento=μF=μmg ⇒ W=μmgd= 0.25 · 0.5mg=0.125mg
Como esta energía disipada es menor que la energía cinética inicial el bloque llegará al punto F con una energía cinética igual a la diferencia entre la inicial y la disipada y seguirá desplazándose hacia el punto G hasta que su velocidad se anule, lo que corresponde a la máxima deformación del muelle.
Esa energía cinética que el bloque tenía en F en parte se disipa por rozamiento y en parte se queda almacenada en el resorte, que se comprime Δl:
![]()
(0.75-0.125) · 0.25 · 9.8=0.25 · 0.25 · 9.8Δl+100Δl2 ⇒ 100Δl2+0.6125Δl-1.5312=0
![]()
Eliminamos la solución negativa, ya que implicaría que el resorte está estirado y no comprimido. Por tanto:
Δl=12.07 cm