Problema de Movimiento Oscilatorio

Aparece en la convocatoria FEB2001

Un objeto de masa 2 kg oscila en el aire con una frecuencia angular de 5 rad/s. Para t=0 s la posición del objeto es 10 cm y su velocidad en este momento de -25 cm/s. a) Determinar la amplitud y la constante de fase para este movimiento. Escribir la ecuación que define el movimiento. b) A continuación introducimos el sistema en un medio viscoso que ofrece una resistencia de 5.25v N, siendo v la velocidad del objeto. Razonar el tipo de amortiguamiento. Calcular el parámetro de amortiguamiento, la frecuencia angular de la oscilación y la ecuación del movimiento sabiendo que para un tiempo nulo su posición es de 10 cm y para t=2 s de 0.051 cm. c) Si además, en ese medio viscoso le aplicamos al objeto una fuerza sinusoidal de F=2.5cos4t N, calcular la amplitud de las oscilaciones, la impedancia del oscilador y el valor de la frecuencia angular de la fuerza impulsora para la cual la amplitud alcanza su valor máximo.

a) φ0=-0.35π rad; A=-11.18 cm; y=-11.18sen(5t-0.35π)
b) MOVIMIENTO SUBAMORTIGUADO; β=1.3125 rad/s; =4.82 rad/s;
y=-50.04e-1.3125tωsen(4.82t-0.201)
c) A=9.04 cm; Z=6.91 Ns/m; ωR=4.64 rad/s

a) La ecuación del movimiento será del tipo:

y=Asen(ωt+φ0)=Asen(5t+φ0)

siendo A la amplitud y φ0 la fase inicial. La velocidad será por tanto:

Tenemos las condiciones iniciales:

t=0 ⇒ y=10 cm ⇒ y=Asen(5t+φ0) ⇒ 10=Asenφ0

Dividiendo las dos expresiones:

φ0=-0.35πrad

Y de una cualquiera de las dos ecuaciones podemos determinar la amplitud:

A=-11.18 cm

La ecuación que define el movimiento, por tanto, será:

y=Asen(5t+φ0)=-11.18sen(5t-0.35π)

y=-11.18sen(5t-0.35π)

 

b) La fuerza de amortiguamiento es del tipo:

F=γv

siendo γ=5.25 Ns/m la constante de amortiguamiento. Para determinar el tipo de amortiguamiento tendremos que calcular el parámetro de amortiguamiento β. Tendremos pues:

Como βω0 el movimiento es subamortiguado.

MOVIMIENTO SUBAMORTIGUADO

El parámetro de amortiguamiento ya lo hemos determinado:

β=1.3125 rad/s

La frecuencia angular de la oscilación, teniendo en cuenta el tipo de amortiguamiento, será:

ω=4.82 rad/s

La ecuación del movimiento será del tipo:

y=A0e-βtsen(ωt+φ0)

donde A0 es la amplitud inicial del movimiento. Conocemos varios parámetros, que sustituyendo nos dan la ecuación:

y=A0e-βtsen(ωt+φ0)=A0e-1.3125tsen(4.82t+φ0)

Para determinar las dos constantes A0 y φ0 tenemos las condiciones iniciales:

t=0 ⇒ y=10 cm ⇒ y=A0e-1.3125tsen(4.82t+φ0) ⇒ 10=A0senφ0

t=2 s ⇒ y=0.051 cm ⇒ y=A0e-1.3125tsen(4.82t+φ0)
0.051=A0e-1.3125 · 2sen(4.82 · 2+φ0)

Nos queda pues el sistema de ecuaciones:

10=A0senφ0

0.051=A0e-2.625sen(9.64+φ0)

De la primera ecuación:

Y sustituimos en la segunda:

Desarrollamos el seno de la suma:

tgφ0=-0.204 ⇒ φ0=-0.201 rad

Y la amplitud inicial será:

Por tanto la ecuación del movimiento es:

y=A0e-1.3125tsen(4.82t+φ0)=-50.04e-1.3125tsen(4.82t-0.201)

y=-50.04e-1.3125tsen(4.82t-0.201)

 

c) La amplitud de las oscilaciones será:

A=9.04 cm

La impedancia será:

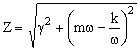
Para determinar la constante del resorte podemos utilizar la frecuencia angular del movimiento sin amortiguar:

Sustituyendo:

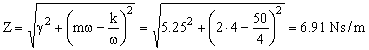
Z=6.91 Ns/m

Por último, la frecuencia de la resonancia es:

ωR=4.64 rad/s