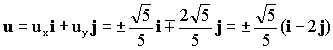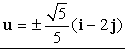a) 27^o16´

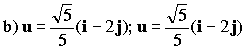
a) Los vectores AB y CD son:

AB=2i+j+2k; CD=4i+4j+2k

Los módulos de ambos vectores son:

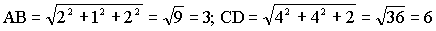
Y el ángulo que forman ambos vectores lo podemos obtener a partir de la definición de producto escalar, ya vista en otros problemas:

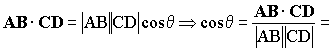
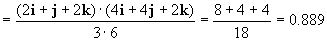
θ=27.27^º

 

b) Nos hablan de un vector unitario que está contenido en el plano XY, luego será de la forma:

u=u_xi+u_yj

Como es un vector unitario, su módulo vale la unidad:

u_x²+u_y²=1

Además, este vector es perpendicular al vector AB, luego el producto escalar de estos dos vectores será nulo (el ángulo que forman es de 90^º y su coseno será cero):

u · AB=0 ⇒ (u_xi+u_yj) · (2i+j+2k)=0 ⇒ 2u_x+u_y=0
u_y=-2u_x

Sustituyendo esta expresión en la del módulo del vector unitario:

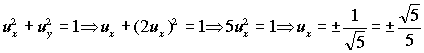
Y entonces:

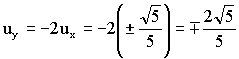
Entonces el vector unitario buscado es: