D=2B X A
(A+B)x(A–B) = AxA – AxB + BxA – BxB=2BxA
puesto que el producto vectorial de un vector por sí mismo es nulo y –AxB = BxA.
Si ahora expresamos los vectores A y B en función de sus componentes cartesianas serán:
A=Axi+Ayj+Azk; B=Bxi+Byj+Bzk
Por tanto su suma y su diferencia son:
A+B= Axi+Ayj+Azk+Bxi+Byj+Bzk=(Ax+Bx)i+(Ay+By)j+(Az+Bz)k
A–B= Axi+Ayj+Azk-Bxi-Byj-Bzk=(Ax-Bx)i+(Ay-By)j+(Az-Bz)k
El producto vectorial de estos dos vectores es:
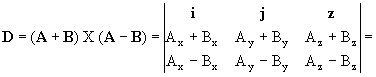
=[
(Ay+By)(Ax-Bx)-(Ax+Bx)(Ay-By)]
¡+ [
(Az+Bz)(Ax-Bx)-(Ax+Bx)(Az-Bz)]
j+
+[
(Ax+Bx)(Ay-By)-(Ay+By)(Ax-Bx)]
k+
=(AyAz-AyBz+ByAz-ByBz-AzAy+AzBy-BzAy+BzBy)i+
+(AzAx-AzBx+BzAx-BzBx-AxAz+AxBz-BxAz+BxBz)j+
+(AxAy-AxBy+BxAy-BxBy-AxAy+AyBx-ByAx+ByBx)k=
=(-2AyBz+2ByAz)i+(-2AzBx+2BzAx)j+(-2AxBy+2BxAy)k=
=2(ByAz-AyBz)i+2(BzAx-AzBx)j+2(BxAy-AxBy)k=2B X A
D=2B X A