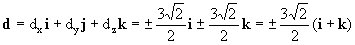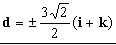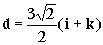
Determinaremos en primer lugar el vector suma:
S=a+b+c=i+2j+k+2i–j+k+i–j+2k=4i+4k
Llamaremos d al vector que buscamos, que será del tipo:
d=dxi+dyj+dzk
Como los vectores S y d son paralelos, formarán un ángulo de 0o, cuyo seno es cero. El producto vectorial de S por d será el producto de los módulos de ambos vectores por el seno del ángulo que forman. Como dicho seno es nulo, el producto vectorial de S y d debe ser cero. Tendremos la ecuación:
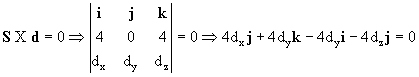
Como tenemos un vector nulo, deberán ser nulas por separado cada una de sus componentes, es decir:
-4dy=0 ⇒ dy=0
4dx-4dz=0 ⇒ dx-dz=0 ⇒ dx=dz
4dy=0 ⇒ dy=0
Puede observarse que las ecuaciones primera y tercera nos conducen al mismo resultado. Nos queda pues la ecuación:
dx=dz
Pero además sabemos que el módulo del vector d vale 3, luego:
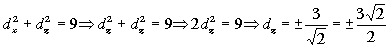
Y por tanto:
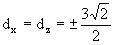
Luego el vector d será: