a) 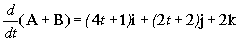
b) 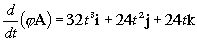
c) 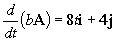
d) 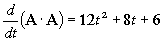
e) 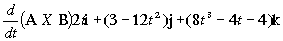
f) 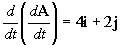
a) El vector A+B será:
A+B=2t2i+2tj+3k+(t+2)i+t2j+2tk=(2t2+t+2)i+(t2+2t)j+(2t+3)k
Y la derivada:
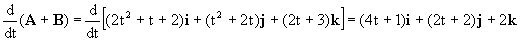
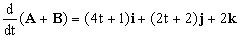
b) El vector φA es:
φA=(4t2)( 2t2i+2tj+3k)=8t4i+8t3j+12t2k
Y su derivada:
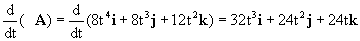
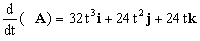
c) El vector bA vale:
bA=2(2t2i+2tj+3k)=4t2i+4tj+6k
Y su derivada:
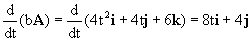
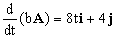
d) El producto escalar de A · B es:
A · B=(2t2i+2tj+3k) · [(t+2)i+t2j+2tk]
=2t3+4t2+2t3+6t=4t3+4t2+6t
Y derivando:
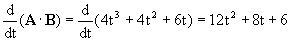
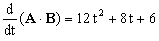
e) El producto vectorial es:
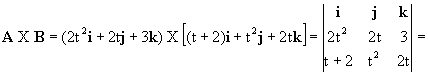
=(4t2-3t2)i+(3t-4t3)j+(2t4-2t2-4t)k=-t2i+(3t-4t3)j+(2t4-2t2-4t)k
Y derivando:
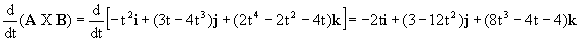
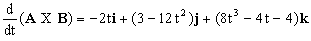
f) Y ahora la derivada del vector A es:
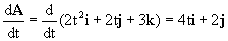
Y volviendo a derivar:
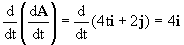
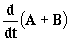 ; b)
; b) 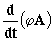 ; c)
; c) 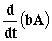 ; d)
; d) 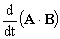 ; e)
; e) 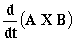 ; f)
; f) 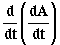 .
.