a) vm/O=(3+v´x)i
b) v´x1=5/2 m/s; v´x2=5 m/s; v´x3=15/2 m/s
c) (vm/O)1=11/2 m/s; (vm/O)2=8 m/s; (vm/O)3=21/2 m/s
d) aS=aS’=5/2 m/s2
a) Como el movimiento es unidimensional (sólo existe movimiento en el eje X) resolveremos el problema escalarmente. Supondremos además que el sistema S es un sistema de referencia fijo, es decir:
vO=0
Tenemos como dato conocido la velocidad de la masa respector de O´, que es v´x:
vm/O´=v´x
La velocidad de O’ respecto de O es:
vO´/O=3 m/s=vO´-vO ⇒ vO=vO´-3
Además, la velocidad de la masa respecto del origen O´ es:
vm/O´=vm-vO´ ⇒ vm=vm/O´+vO´=v´x+vO´
Por tanto, la velocidad de la masa, respecto del origen O, será:
vm/O=vm/O´+vO´/O=v´x+3
vm/O=v´x+3
b) La aceleración a que está sometida la masa, teniendo en cuenta la segunda ley de Newton, es:
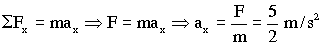
El sistema S´ no está acelerado respecto de S, luego la aceleración de la masa es idéntica en los dos sistemas:
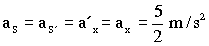
Como la aceleración es constante el movimiento es rectilíneo uniformemente acelerado. Tendremos entonces que en el sistema S´:
v´x=axt
Por tanto para t=1 s:
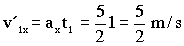
v´1x=5/2 m/s
Para t=2 s:
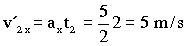
v´2x=5 m/s
Y para t=3 s:
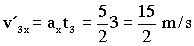
v´3x=15/2 m/s
c) Del apartado a) tenemos ya que:
vm/O=v´x+3
Entonces, sustituyendo por lo que hemos encontrado en el apartado anterior, para t=1 s:
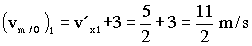
(vm/O)1=11/2 m/s
Para t=2 s:
(vm/O) 2=v´x2+3=5+3=8 m/s
(vm/O)2=8 m/s
Y para t=3 s:
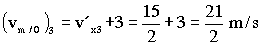
(vm/O)3=21/2 m/s
d) Como ya hemos dicho antes, el sistema S´ no está acelerado respecto de S, luego la aceleración de la masa m es idéntica en los dos sistemas:
as=aS´=5/2 m/s