Problema de Cinemática de la Partícula

El movimiento plano de una partícula viene descrito en un cierto sistema de referencia por las ecuaciones x=8t, y=6t-t2. Un segundo sistema de referencia se mueve con una velocidad constante v0=8i respecto al primero, y coincide con él en el instante t=0. Calcular la velocidad y la aceleración de la partícula respecto de ambos sistemas de referencia.

Respecto del primer sistema: v1=8i+(6-2t)j; a1=-2j
Respecto del segundo sistema: v1/2=(6-2t)j; a1/2=-2j

Respecto del primer sistema el vector de posición es:

rp/1=8ti+(6t-t2)j

Por tanto respecto del primer sistema la velocidad será:

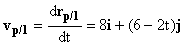
vp/1=8i+(6-2t)j

Y la aceleración respecto de este primer sistema:

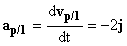
ap/1=-2j

Ahora tendremos que el sistema 2 se mueve respecto del 1 con una velocidad:

v2/1=v0=8i

Y entonces la velocidad de la partícula respecto del sistema 2 será:

vp/2=vp/1–v2/1=8i+(6-2t)j-8i=(6-2t)j

vp/2=(6-2t)j

La aceleración del sistema 2 respecto del 1 es nula, luego la aceleración de la partícula es la misma medida respecto del sistema 2 que respecto del sistema 1:

ap/1=-2j