v=1.5 km/h
Vamos a resolver el problema de dos formas. En primer lugar vamos a referir el movimiento a un sistema solidario a la orilla del río. Podemos asegurar que tanto el agua del río como el bote en el tramo considerado realizan movimientos rectilineos y uniformes. Llamamos «t» al tiempo (en horas) que transcurre desde que el hombre pierde la botella hasta que la recupera, «s» al espacio (en km) recorrido desde el puente hasta que el hombre se da cuenta que ha perdido la botella y da la vuelta, «va» a la velocidad del agua y «vr» a la velocidad del bote respecto al agua.
El espacio que recorre la botella es igual a la velocidad que lleva (que es la misma del agua) multiplicada por el tiempo que transcurre desde que se cae del bote hasta que el hombre la encuentra nuevamente:
1 km =vat
A la ida, durante los 20 minutos en que no se da cuenta de que ha perdido la botella, el hombre recorre en su bote un espacio s, con una velocidad absoluta que será vr-va (hay que tener en cuenta que va río arriba). El tiempo en horas será:
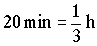
Entonces tendremos:
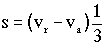
A la vuelta, desde que se da cuenta de que ha perdido la botella hasta que la encuentra, el hombre recorre un espacio s+1 (ya que la encuentra 1 km más abajo), con una velocidad absoluta vr+va (ahora va a favor de la corriente), y tarda un tiempo t-1/3. Entonces:
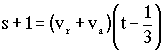
Desarrollando la última ecuación tendremos:
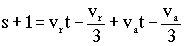
De la otra:
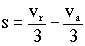
Sustituyendo en la primera:
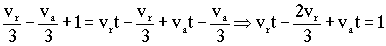
Sabemos de la primera expresión que:
vat=1
Por lo tanto obtenemos:
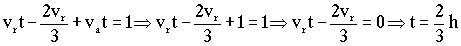
Y conocido el tiempo:
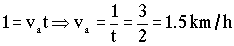
va=1.5 km/h
Ahora vamos a referir el movimiento a un sistema solidario con el agua del río. En este caso el agua, respecto a dicho sistema, estaría en reposo y la botella también. El movimiento del bote seria rectilineo y uniforme con una velocidad vr.
Si el bote se aleja de la botella con una velocidad vr durante un tiempo de 20 min y luego se acerca a la botella con la misma velocidad, invertirá en llegar hasta ella el mismo tiempo, es decir, otros 20 min. El tiempo que transcurre, por tanto, desde que pierde la botella hasta que la recupera es de 40 min. En horas:
t=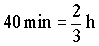
En este caso tendremos:
velocidad del agua: 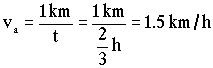
va=1.5 km/h