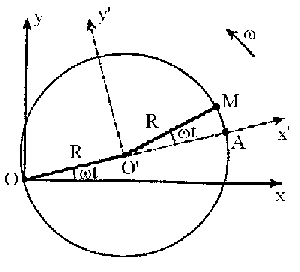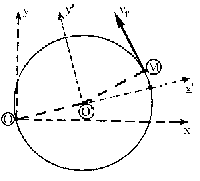
Empezaremos por la velocidad relativa. La velocidad relativa del punto M es la que tiene por el hecho de recorrer la circunferencia con velocidad constante. Dicha velocidad v_r=ωxO’M será tangente a la circunferencia en el punto dado y su sentido es el de avance de la partícula.

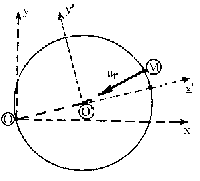Del mismo modo, la aceleración relativa es la que tiene el punto M por recorrer la circunferencia con velocidad angular constante. En general, en el movimiento circular la aceleración tiene dos componentes, normal y tangencial. En este caso la tangencial es nula ya que el módulo de la velocidad es constante, luego la aceleración relativa sólo tiene componente normal, en la dirección del radio de curvatura y apuntando hacia el centro de curvatura.

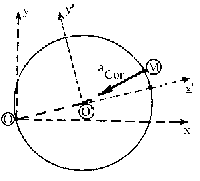La aceleración de Coriolis es:

a_Cor=2w
X v_r

 

Este vector es perpendicular al plano formado por ω y v_r, es decir, en la dirección del radio O´M, y sentido el dado por la regla del sacacorchos cuando se lleva ω sobre v_r por el camino más corto (dirigido hacia O´).

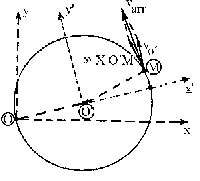La velocidad de arrastre es:

v_arr=v_O´+ω
X O´M=ωXOO’+ωXO’M=ωX(OO’+O’M)

v_O´ es la velocidad del punto O´, que realiza un movimiento circular y uniforme en torno a O. Dicha velocidad será por tanto tangente a la trayectoria en ese punto (perpendicular al radio OO´) y sentido el de avance del punto O´. El término ω X O´M es perpendicular al plano formado por ambos vectores, es decir, tiene la misma dirección que la velocidad relativa, y su sentido aplicando la regla del sacacorchos, el del movimiento. La velocidad de arrastre será la composición de estos dos vectores.

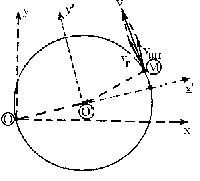
La velocidad absoluta es:

v=v_arr+v_r=ω X OM+ω X O’M

Tendríamos que componer estos dos vectores que ya hemos dibujado antes.

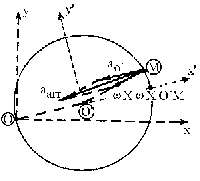La aceleración de arrastre vale:

a_arr=a_O´+α X O´M+ω X ω X O´M

 

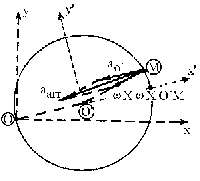El punto O´ hemos dicho que realiza un movimento circular uniforme en torno a O. Como la velocidad angular es constante, la aceleración angular es nula (α=0) luego el segundo sumando de esa expresión es nulo y nos queda:

a_arr=a_O´+ω X ω X O´M

El punto O´ sólo tiene aceleración normal o centrípeta (la tangencial es nula puesto que el módulo de la velocidad permanece constante). Dicha aceleración tiene la dirección del radio de curvatura (OO´) y apunta hacia el centro de curvatura (hacia O). El vector ω X ω X O´M es un vector perpendicular al plano formado por ω y por ω X O´M, es decir, tiene la dirección del radio O´M y sentido apuntando hacia O´. La composición de estos dos vectores nos da la aceleración de arrastre.

Y por último, la aceleración absoluta:

a=a_O´+a_arr+a_Cor

Se deben componer estos tres vectores que ya hemos representado antes.