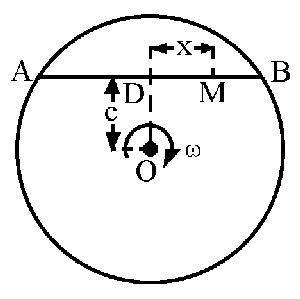
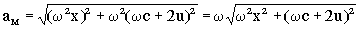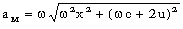Tomaremos como sistema de referencia un eje X coincidente con la recta AB y positivo hacia B, un eje Y que coincide con la recta OD y positivo hacia D y un eje Z perpendicular a ambos y positivo hacia fuera. Como el sistema de referencia está en rotación, la velocidad absoluta del punto M es:
vM=vO+ω X OM+vr
El punto O es un punto fijo por lo que:
vO=0
La velocida angular tiene sentido horario luego:
ω=-ωk
El vector de posición OM tiene en ese momento dos componentes que valen, tal como hemos elegido los ejes:
OM=xi+cj
Y la velocidad relativa me dicen que vale u, y además como tendría la dirección de la cuerda AB sólo tiene componente en X:
vr=ui
Sustituyendo en la expresión de la velocidad absoluta:

En módulo:
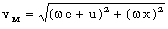
Para la aceleración tendremos:
aM=aO+α X OM-ω2OM+2ω X vr+ar
Como el punto O es un punto fijo:
aO=0
El disco gira con velocidad angular constante, luego:
α=0
Y en cuanto a la aceleración relativa, como la velocidad relativa es constante tanto en módulo como en dirección y sentido:
ar=0
Por tanto sustituyendo todo:
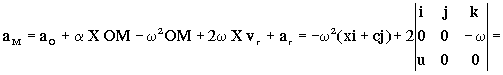
=-ω2xi-ω2cj-2ωuj=-ω2xi-(ω2c+2ωu)j=-ω2xi-ω(ωc+2u)j
En módulo: