aAX=-72.5 cm/s2; aAY=225 cm/s2
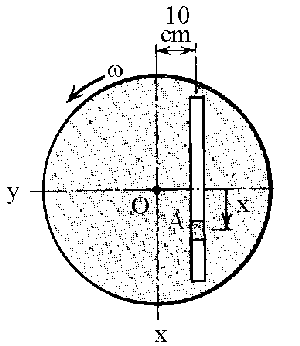
Tomaremos el sistema de ejes coordenados que nos indican en el enunciado. Habrá que tener en cuenta que el triedro no es directo y que por tanto no podemos utilizar el determinante a la hora de hacer los productos vectoriales, sino que habrá que usar, por ejemplo, la regla del pulgar de la mano derecha.
La aceleración absoluta del punto A es:
aA=aO+α X OA-ω2OA+2ω X vr+ar
Vamos a ir determinando cada uno de los términos. El punto O es un punto fijo, luego no tiene ni velocidad ni aceleración:
aO=0
La aceleración angular es:
α=-10k
El vector de posición, tal como están los ejes:
OA=7.5i-10j
La velocidad angular:
ω=5k
La velocidad relativa es la que tiene la corredera dentro del sistema de referencia en rotación. Dentor de este sistema la corredera está confinada a moverse en la ranura, es decir, sólo en el eje X, con una velocidad que es:
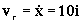
Del mismo modo, la aceleración relativa es:
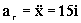
Por tanto, sustituyendo:
aA=aO+α X OA-ω2OA+2ω X vr+ar=(-10k) X (7.5i-10j)-52(7.5i-10j)+2(5k) X (10i)+15i=
=75j+100i-187.5i+250j-100j+15i=-72.5i+225j
Por tanto las componentes de la aceleración son en módulo:
aAX=72.5 m/s2
aAY=225 m/s2
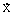 =10 cm/s y
=10 cm/s y  =15 cm/s2.
=15 cm/s2.