a) v_A/B=-2.78i-5.56j m/s; 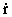=-5.90 m/s; 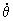=-4.63*10^-4 rad/s
b) a_A/B=0.0198i m/s²; 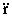=0.014 m/s²; 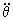=-4.59*10^-6 rad/s²
c) v_rel=-2.78i+11.12j; a_rel=0.010i

a) En primer lugar pasamos todo al Sistema Internacional:

v_A=20 km/h=5.56 m/s; v_B=10 km/h=2.78 m/s; a_B=2 km/hmin=9.3 · 10^-3 m/s²

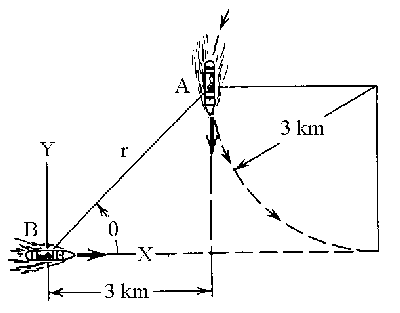
El barco A está moviéndose en una trayectoria circular con velocidad constante, luego tendrá aceleración normal (la tangencial será nula ya que el módulo de la velocidad es constante) que vale:

El ángulo θ mostrado en el dibujo vale:

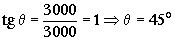
Y la distancia r:

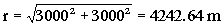
Una vez determinad la geometría del problema, vamos a representar ahora estas velocidades y aceleraciones en un gráfico. En el mismo aparecen también los ejes X e Y. Además, para determinar los valores de las derivadas temporales de r y θ utilizaremos coordenadas polares planas, por lo que representamos también en el gráfico los vectores unitarios u_r y u_θ en la dirección de crecimiento de r y perpendicular a dicho vector y en el sentido de crecimiento de θ.

 

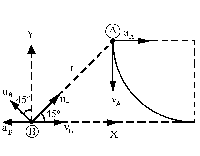
El barco A está moviéndose en una trayectoria circular con velocidad constante. La velcoidad por tanto será tangente a la trayectoria en el punto dado y sentido el de avance del móvil, es decir, vertical y hacia abajo. Como el movimiento es circular y uniforme, la aceleración de A serán normal o centrípeta, y tendrá la dirección del radio de curvatura y apuntando hacia el centro de curvatura. La velocidad del barco B es horizontal y hacia la derecha, ya que el movimiento de este barco es unidimensional. Su aceleración será horizontal pero hacia la izquierda, porque el movimiento es decelerado. Vectorialmente entonces tenemos todas, que son:

v_A=-5.56j: a_A=0.0105i; v_B=2.78i; a_B=-9.3 · 10^-3i

 

Si queremos la velocidad de A respecto de B, tendremos que B es un sistema de referencia en traslación, luego: v_A/B=v_A–v_B=-5.56j-2.78i

v_A/B=-2.78i-5.56j m/s

Ahora, si expresamos esta velocidad relativa en coordenadas polares planas tendremos:

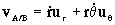
Los vectores unitarios u_r y u_θ son: u_r=cos45^Oi+sen45^Oj; u_θ=-sen45^Oi+cos45^Oj

Si sustituímos todo en la expresión de la velocidad relativa de A respecto de B tendremos:

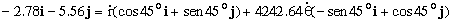
Igualamos por separado las componentes en X y en Y:

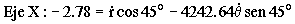
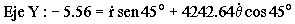
Teniendo en cuenta que el seno y el coseno de 45^º son iguales, si restamos estas dos ecuaciones nos queda:

Y despejando de una cualquiera de las otras el valor de la derivada de r tendremos:

b) Vamos a hacer lo mismo con la aceleración. Puesto que el barco B es un sistema de referencia en traslación, la aceleración de A respecto de B será:

a_A/B=a_A–a_B=0.0105i+9.3 · 10^-3i=0.0198i

a_A/B=0.0198i m/s²

 

Y ahora expresamos esta aceleración relativa en coordenadas polares planas, con lo que tenemos:

Sustituyendo en la ecuación ahora todo lo que conocemos, y efectuando operaciones se llega a:

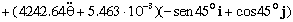
Igualamos por separado las componentes en X y en Y:

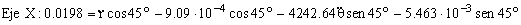
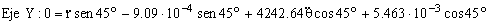
De la segunda ecuación podemos obtener una relación entre las dos incógnitas:

Si sustituímos esta expresión en la ecuación del eje X y operamos, llegaremos a la expresión:

Y sustituyendo en la expresión de :

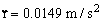
c) Si tenemos al observador situado en A, el sistema de referencia está en rotación, con lo cual tendremos:

v_B=v_A+ω X AB+v_r ⇒ v_r=v_B–v_A-ω X AB

La velocidad angular del barco A podemos determinarla teniendo en cuenta su velocidad lineal:

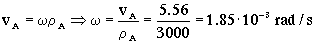
Vectorialmente:

ω=1.85 · 10^-3k

Y el vector de posición: AB=-3000i-3000j

 

Sustituyendo todo:

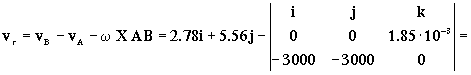
=2.78i+5.56j+5.56j-5.56i=-2.78i+11.12j

v_r=-2.78i+11.12j m/s

Para la aceleración relativa tendremos exactamente lo mismo en aceleraciones. Puesto que el barco A es un sistema de referencia en rotación:

a_B=a_A+α X AB-ω²AB+2ω X v_r+a_r ⇒ a_r=a_B-α X AB+ω²AB-2ω X v_r

Como el barco A se mueve con velocidad angular constante, la aceleración angular será nula:

ω=cte ⇒ α=0

Sustituyendo entonces tendremos:

a_r=0.010i m/s²