v_rel=-721.92i+160j-262.656k km/h; a_rel=-72177.84i-73769.58j-26266.53k km/h²

Tomaremos como sistema de referencia el que aparece en el enunciado del problema. Podemos trabajar en principio con las velocidades en km/h y la velocidad angular en rad/h. El avión A es un sistema de referencia en rotación, por lo que si queremos determinar la velocidad relativa de B respecto de A tendremos:

v_B=v_A+ω X AB+v_r ⇒ v_r=v_B–v_A-ω X AB

Las velocidades de los aviones A y B son:

v_A=480j; v_B=640j

El avión A está rotando. Teniendo en cuenta su velocidad lineal podemos determinar la angular:

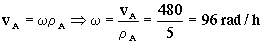
Si la proyectamos sobre los ejes marcados en el problema:

ω=-96(-sen20^Oi+cos20^Ok)=32.832i-90.24k

Y el vector de posición, en km, es:

AB=8j

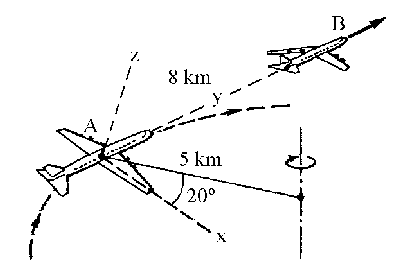
Sustituyendo todo, la velocidad relativa es:

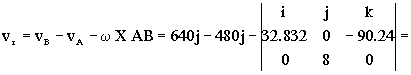
=640j-480j-262.656k-721.92i=-721.92i+160j-262.656

v_r=-721.92i+160j-262.656k km/h

Para la aceleración relativa haremos exactamente lo mismo. Dado que el avión A es un sistema de referencia en rotación:

a_B=a_A+α X AB+ω X ω X AB+2ω X v_r+a_r ⇒ a_r=a_B–a_A-α X AB-ω X ω X AB-2ω X v_r

El avión B vuela en línea recta con velocidad constante, luego su aceleración será nula:

a_B=0

El avión A vuela en círculo con velocidad angular constante, luego de las dos componentes de aceleración que puede tener (tangencial y normal) sólo tendría la normal, ya que la tangencial es nula (el módulo de la velocidad permanece constante). Dicha aceleración valdrá:

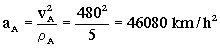
Y vectorialmente tiene la dirección del radio de curvatura y apuntando hacia el centro de curvatura, es decir:

a_A=a_A(cos20^Oi+sen20^Ok)=46080(cos20^Oi+sen20^Ok)=43301.04i+15760.29k

Como el avión A se mueve con velocidad angular constante, la aceleración angular es nula:

ω=cte ⇒ α=0

Y sustituyendo tendremos:

a_r=a_B–a_A-α X AB-ω X ω X AB-2ω X v_r=-43301.04i-15760.29k–

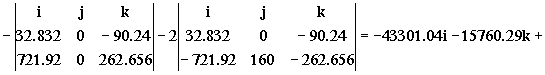
+65146.06j+8623.52j-130292.12j-10506.24k-28876.8i-17247.04j=-72177.84i-73769.58j-26266.53k

a_r=-72177.84i-73769.58j-26266.53k km/h²