a1=4.2j m/s2; a2=-0.6i+3.6j m/s2; a3=3.0j m/s2; a4=0.6i+3.6j m/s2
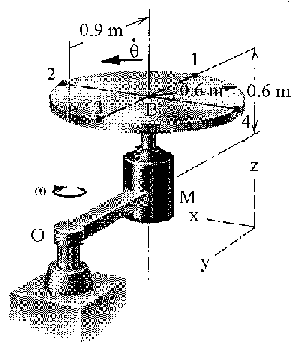
Tomaremos el sistema de ejes que hay en la figura. Tenemos como sistema de referencia el brazo, y a él referiremos el movimiento del disco. Tenemos pues un sistema de referencia en rotación.
La aceleración del punto 1 será:
a1=aO+α X O1+ω X ω X O1+2ω X vr1+ar1
El punto O es un punto fijo, que no tiene ni velocidad ni aceleración, luego:
aO=0
La velocidad angular del brazo es constante, luego su aceleración angular es nula:
ω=cte ⇒ α=0
La velocidad angular, que nos valdrá para todos los puntos es:
ω=-2k
El vector de posición:
O1=-1.5j+0.6k
El primer producto vectorial ω X O1 será:
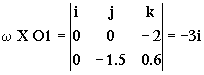
La velocidad relativa será la que tiene el punto 1 por estar en el disco. En el disco el movimiento es circular y uniforme, luego la velocidad será tangente a la trayectoria en ese punto:
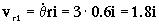
Y la aceleración relativa, por ser el movimiento circular y uniforme, será normal o centrípeta (la tangencial es nula por ser el módulo de la velocidad constante) y tendrá la dirección del radio de curvatura y apuntando hacia el centro de curvatura:
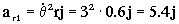
Sustituyendo todo:
a1=aO+α X O1+ω X ω X O1+2ω X vr1+ar1= ω X ω X O1+2ω X vr1+ar1=
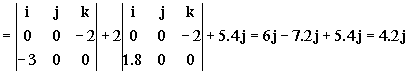
a1=4.2j m/s2
Vamos haciendo lo mismo para los otros puntos, teniendo en cuenta que me valen la aceleración del punto O (nula), la aceleración angular (nula) y la velocidad angular. Para el punto 2 tendré:
a2=aO+α X O2+ω X ω X O2+2ω X vr2+ar2= ω X ω X O2+2ω X vr2+ar2
Los parámetros que varían serán:
O2=0.6i-0.9j+0.6k
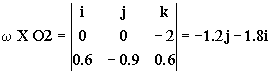
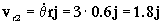
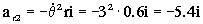
Y sustituyendo:
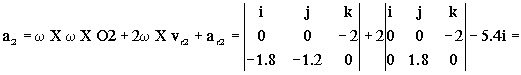
=-2.4i+3.6j+7.2i-5.4i=-0.6i+3.6j
a2=-0.6i+3.6j m/s2
Para el punto 3:
a3=aO+α X O3+ω X ω X O3+2ω X vr3+ar3= ω X ω X O3+2ω X vr3+ar3
Los términos que nos faltan son:
O3=-0.3j+0.6k
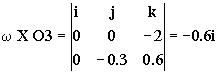
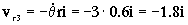
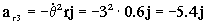
Sustituyendo todo:
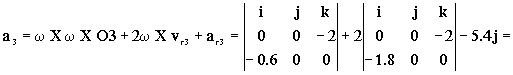
=1.2j+7.2j-5.4j=3j
ar3=3j m/s2
Por último, para el punto 4:
a4=aO+α X O4+ω X ω X O4+2ω X vr4+ar4= ω X ω X O4+2ω X vr4+ar4
Donde tendremos:
O4=-0.6i-0.9j+0.6k
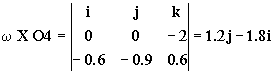
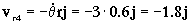
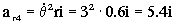
Y sustituyendo todo:
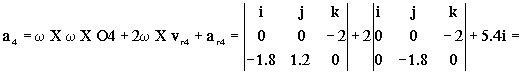
=3.6j+2.4i-7.2i+5.4i=0.6i+3.6j
a4=0.6i+3.6j m/s2
 =3 rad/s relativa al armazón del motor y brazo solidario OM. Simultáneamente, el brazo se pone en rotación en el sentido de las agujas del reloj con celeridad angular constante ω=2 rad/s. Determinar la aceleración absoluta de cada uno de los cuatro puntos del disco en las posiciones indicadas.
=3 rad/s relativa al armazón del motor y brazo solidario OM. Simultáneamente, el brazo se pone en rotación en el sentido de las agujas del reloj con celeridad angular constante ω=2 rad/s. Determinar la aceleración absoluta de cada uno de los cuatro puntos del disco en las posiciones indicadas.