acf=ω2RcosΦ, en dirección normal al eje de giro y sentido desde dicho eje hacia fuera
aCor=2ωv´senΦ, en dirección O-E en el hemisferio Norte y E-O en el hemisferio Sur
aC=-0.024 m/s2; aCor=± 0.0516 m/s2.
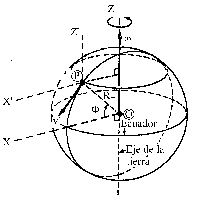
Tomaremos un sistema de ejes coordenados como el que se indica en la figura. El eje Z coincide con el eje de rotación de la Tierra, y los ejes X e Y son perpendiculares a él y están tomados de tal modo que la velocidad relativa v´ no da proyección sobre el eje Y. En el dibujo hemos colocado a la partícula en el hemisferio Norte, de modo que el ángulo Φ es positivo. Cuando esté en el hemisferio Sur sólo habrá que tomar este ángulo como negativo. Llamaremos O al origen de la Tierra y P al punto en que se encuentra la partícula, de modo que el vector de posición será OP. Con estos ejes la dirección Norte está marcada por el sentido positivo del eje Z, el Sur es el sentido negativo del eje Z, el Este coincide con el sentido positivo del eje Y y el Oeste con el sentido negativo del eje Y.
La aceleración centrífuga y la centrípeta son iguales y de signo contrario. La aceleración centrípeta vale:
acp=ω X ω X OP
Vamos a ver cuánto vale cada uno de estos términos. La velocidad angular tiene la dirección del eje Z positiva, ya que la Tierra rota en torno a su eje en sentido antihorario. Entonces:
ω=ωk
Y el vector de posición es, denominando RT al radio de la Tierra:
OP=RTcosΦi+RTsenΦk
Sustituyendo:


acp=-ω2RTcosΦi
Para hacer el cálculo numérico tendremos que determinar la velocidad angular de la Tierra. La Tierra tarda 24 horas en dar una vuelta completa alrededor de sí misma. Además, en ese mismo tiempo gira un ángulo θ alrededor del Sol que vale:
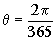
ya que en torno al Sol la Tierra tarda 365 días en dar una vuelta completa. De este modo la velocidad angular de la Tierra será el cociente entre el ángulo girado en un día dividido por el tiempo, es decir:
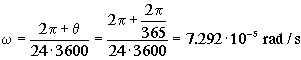
Y el radio de la Tierra:
RT=6370 km=6.37 · 106 m
Numéricamente, cuando la partícula está en el hemisferio Norte:
acp=-ω2RTcosΦi=-(7.292 · 10-5)2 · 6.37 · 106cos45Oi=-0.024i m/s2
La dirección del eje X es la perpendicular al eje de rotación; como es negativa, estará dirigida hacia el eje de rotación. Por tanto la aceleración centrífuga es la contraria a la centrípeta:
acf=-acp=0.024i m/s2
En módulo:
acf=0.024 m/s2
Su dirección es la normal al eje de rotación y sentido desde el eje de rotación hacia fuera.
Si la partícula se encuentra en el hemisferio Sur lo único que cambia es el signo del ángulo y tendremos:
acp=-ω2RTcosΦi=-(7.292 · 10-5)2 · 6.37 · 106cos(-45º)i=-0.024i m/s2
Luego las aceleraciones centrípeta y centrífuga no cambian al cambiar la partícula de hemisferio. En el hemisferio Sur:
acf=0.024 m/s2
Su dirección es la normal al eje de rotación y sentido desde el eje de rotación hacia fuera.
Ahora vamos a ver la aceleración de Coriolis. Esta aceleración vale:
aCor=2ω X vr
La velocidad relativa es v´ y podemos ver en el gráfico que vale:
vr=v´=v´senΦi-v´cosΦk
Por tanto la aceleración de Coriolis:

aCor=2ωv´senΦj
La dirección de esta aceleración es la del eje Y. Su sentido depende de si la partícula está en el hemisferio Norte o en el hemisferio Sur. Si se encuentra en el hemisferio Norte y la velocidad relativa es de 500 m/s tendremos:
aCor=2ωv´senΦj=2 · 7.292 · 10-5 · 500sen45Oj=0.0516j m/s2
La dirección del eje Y positivo coincide con el Este, luego cuando la partícula está en el hemisferio Norte la aceleración de Coriolis vale:
aCor=0.0516 m/s2
Y su dirección es de Oeste a Este.
Si la partícula se encuentra en el hemisferio Sur cambia el signo del ángulo y nos queda:
aCor=2ωv´senΦj=2 · 7.292 · 10-5 · 500sen(-45º)j=-0.0516j m/s2
La dirección del eje Y negativo coincide con el Oeste, luego cuando la partícula está en el hemisferio Sur la aceleración de Coriolis vale:
aCor=0.0516 m/s2
Y su dirección es de Este a Oeste.