aCor=1.75*10-4 m/s2 hacia el Oeste; nivel más elevado en la orilla derecha respecto al sentido de la corriente; desnivel de 1.79 cm.
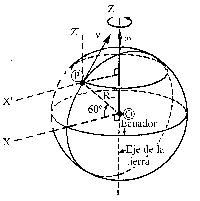
Tomaremos un sistema de ejes coordenados como el que se indica en la figura. El eje Z coincide con el eje de rotación de la Tierra, y los ejes X e Y son perpendiculares a él y están tomados de tal modo que la velocidad relativa vr no da proyección sobre el eje Y. Llamaremos O al origen de la Tierra y P al punto en que se encuentran las partículas del río, de modo que el vector de posición será OP. Con estos ejes la dirección Norte está marcada por el sentido positivo del eje Z, el Sur es el sentido negativo del eje Z, el Este coincide con el sentido positivo del eje Y y el Oeste con el sentido negativo del eje Y.
La aceleración de Coriolis vale:
aCor=2ω X vr
La velocidad angular de la Tierra tiene la dirección del eje Z positiva, ya que la Tierra rota en torno a su eje en sentido antihorario. Entonces:
ω=ωk
La Tierra tarda 24 horas en dar una vuelta completa alrededor de sí misma. Además, en ese mismo tiempo gira un ángulo θ alrededor del Sol que vale:
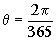
ya que en torno al Sol la Tierra tarda 365 días en dar una vuelta completa. De este modo la velocidad angular de la Tierra será el cociente entre el ángulo girado en un día dividido por el tiempo, es decir:

La velocidad angular entonces vale:
ω=ωk=7.292 · 10-5k
El río respecto de la Tierra corre a una velocidad de 5 km/h, luego ésta será la velocidad relativa. Pasamos en primer lugar la velocidad relativa a m/s:
vr=5 km/h=1.39 m/s
Y vectorialmente podemos ver que:
vr=-vrsenφi+vrcosφk=-1.39sen60Oi+1.39cos60Ok=-1.204i+0.695k
Por tanto la aceleración de Coriolis vale:

En módulo:
aCor=1.75 · 10-4 m/s2
La dirección es de Este a Oeste (dirección negativa del eje Y).

Ahora tenemos que componer un vector igual y opuesto al de la aceleración de Coriolis, es decir, con ese valor pero dirigido hacia el Este, con el vector g, que vale 9.8 m/s2 y está dirigido hacia el centro de la Tierra. El perfil del río es perpendicular al vector resultante de la composición de esos dos vectores. Tendremos lo que aparece en la figura. Podemos ver ya en el gráfico que el perfil está más elevado en el margen derecho:
Más elevado en el margen derecho
El ángulo θ que forma el río con la horizontal podemos determinarlo a través de los vectores –aCor y g y vale:
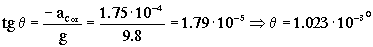
Si llamamos d al desnivel, y tenemos en cuenta que el río tiene 1 km de ancho (llamemos h a esta anchura) ese desnivel valdrá:
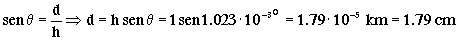
d=1.79 cm