a) a=2.637 m/s2
b) T=2.83 N; tracción
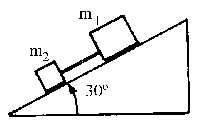
Aislamos conjuntamente los dos bloques y hacemos el diagrama de sólido libre.
Aplicamos la segunda ley de Newton : ΣF= m a
Si tomamos los ejes de coordenadas mostrados en la figura tenemos:
ΣFx= m ax ⇒ (m1 + m2)g sen θ- F1r– F2r = (m1 +m2 )a
Ahora aislamos los bloques por separado y hacemos los diagramas de sólido libre correspondientes.
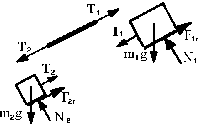
Hemos supuesto que la varilla está sometida a una fuerza tensora de tracción.
Aplicando la segunda ley de Newton a la varilla tenemos:
T2 -T1= m a = 0 porque la masa de la varilla , m, es despreciable ⇒T2=T1
Denominaremos a esta tensión T.
Ahora aplicamos la segunda ley de Newton al bloque de masa m1:
m1 g sen θ+ T1– F1r = m1a.
Como T1=T, la ecuación anterior queda:
m1 g sen θ+ T- F1r = m1 a
Para el otro eje:
N1-m1g cos θ=0 ⇒ N1 = m1 g cos θ
El sistema desliza, luego la fuerza de rozamiento adquiere su valor máximo:
F1r= m1 N = m1 m1 g cos θ
Análogamente en el bloque m2 tenemos:
m2 g sen θ- T2– F2r = m2a.
Como T2=T, tenemos:
m2 g sen θ- T- F2r = m2 a
Y para el otro eje:
N2-m2g cos θ=0 ⇒ N2 = m2 g cos θ
La fuerza de rozamiento en este bloque también adquiere su valor máximo:
F2r= µ2 N = µ2 m2 g cos θ
Sustituyendo los valores anteriores de F1r y F2r en la ecuación:
(m1 + m2)g sen θ- F1r– F2r = (m1 +m2 )a
obtenemos:
(m1 + m2)g sen θ-µ1 m1 g cos θ- µ2 m2 g cos θ= (m1 +m2 )a ⇒
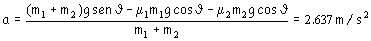
b) Para determinar el valor de la tensión utilizaremos bien la ecuación:
m1 g sen θ+ T- F1r = m1a
ó
m2 g sen θ- T- F2r = m2 a
En esta última ecuación:
T = m2 g sen θ- m2 a +µ2 m2 g cos θ= 2.83 N
T=2.83 N
Como la solución es positiva implica que la tensión que hemos supuesto es correcta, es decir, la varilla está sometida a tracción.
TRACCIÓN