aA=2.36 m/s2 hacia abajo
aB=2.61 m/s2 hacia arriba
aC=0.50 m/s2 hacia abajo
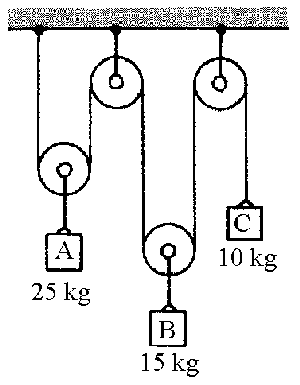
Aislamos los bloques y hacemos los digramas de sólido libre correspondientes. Suponemos que el bloque A se desplaza hacia abajo. Para todos los cuerpos se debe verificar la segunda ley de Newton:
ΣF=ma
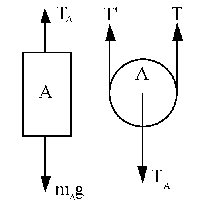
Para el bloque A:
TA-mAg=-mAaA
Para la polea A (la masa mp es despreciable):
TA-T-T´=mpaA=0
Como la polea está rotando:
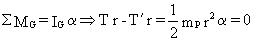
Por tanto:
mAaA=mAg-2T (1)
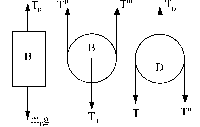
Suponemos que el bloque B se desplaza también hacia abajo. Para este bloque:
mBg-TB=mBaB
En la polea D:
T´´r-Tr=0
porque la masa de la polea es despreciable. Tendremos entonces:
T´´=T
En la polea B:
T´´´r-Tr=0
porque la masa de esta polea también es despreciable. Obtenemos la ecuación:
T´´´=T
Además en la polea:
TB-2T=mpaB=0 ⇒ TB=2T
Por tanto, en el bloque B:
mBaB=mBg-2T (2)
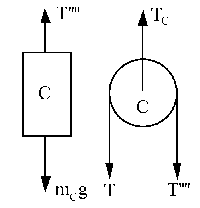
Por último, aislamos el bloque C con la correspondiente polea. Suponemos que el bloque C se desplaza hacia arriba. En la polea C:
Tr-T´´´´r=0 ⇒
T´´´´=T
En el bloque C:
T-mCg=mCaC (3)
De las ecuaciones (1), (2) y (3) sustituyendo los valores conocidos tenemos:
25aA=25 × 9.8-2T
15aB=15 × 9.8-2T
10aC=T-10 × 9.8
Es un sistema de tres ecuaciones y cuatro incógnitas. La cuarta ecuación la determinaremos teniendo en cuenta que los movimientos de los tres bloques están relacionados entre sí.
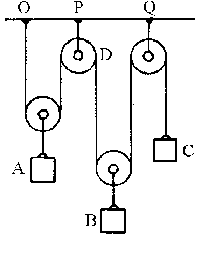
La cuerda que une el bloque C pasando a través de las poleas a un punto fijo O, así como los otros trozos de cuerda, que mantienen los otros bloques unidos a las poleas y los que mantienen a las poleas D y C unidas a puntos fijos (P y Q), son inextensibles por lo que su longitud es constante. Si a las posiciones de los bloques A, B y C con respecto a la linea que une los puntos fijos las denominamos yA, yB e yC respectivamente y teniendo en cuenta lo expuesto en el párrafo anterior tenemos:
2yA+2yB+yC=cte
Derivando dos veces respecto al tiempo (y teniendo en cuenta el sentido del movimiento que hemos asignado a los bloques) obtenemos:
-2 A-2 B+ C=0
Es decir:
2aA+2aB-aC=0
que será la cuarta ecuación. Resolviendo el sistema determinamos
aA=2.36 m/s2
Como la solución es positiva significa que el sentido que le asignamos era correcto.
aA =2.36 m/s2
aB=-2.61 m/s2
El signo negativo indica que el movimiento de este bloque es contrario al supuesto.
aB =2.61 m/s2
aC=-0.5 m/s2
Como antes, el signo negativo de aC nos indica que el desplazamiento inicial supuesto para este bloque es incorrecto.
aC =0.50 m/s2
Es decir, el bloque B sube y el C baja.