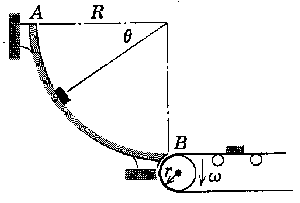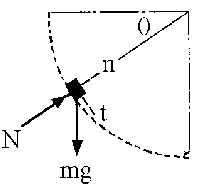
Si la superficie de contacto es lisa, el rozamiento es despreciable, por lo que si aislamos una partícula (un objeto de los que caen) las fuerzas que actúan sobre la misma son su peso y la acción de la superficie circular que es perpendicular a la superficie común. Tiene, por tanto, la dirección del radio de curvatura en el punto considerado y su sentido es hacia el centro de curvatura. El movimiento que describe el pequeño objeto es circular de radio R. El cuerpo por tanto tendrá una aceleración que puede expresarse en componentes intrínsecas (aceleración tangencial y aceleración normal). Como ejes voy a tomar la dirección t (tangente a la trayectoria) y la dirección n (dirección del radio de curvatura). Estas dos direcciones son perpendiculares.

Si aplicamos la 2ª ley de Newton:

ΣF=ma

Tenemos en la dirección tangencial:

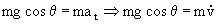
y en la dirección normal:

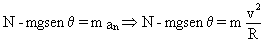
De la primera de esas dos ecuaciones:

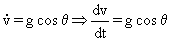
Multiplico y divido por un arco diferencial ds:

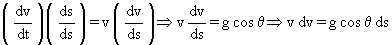
Como el arco es igual al radio por el ángulo:

ds=Rdθ

Por tanto, sustituyendo:

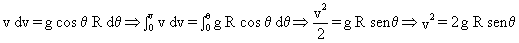
Sustituyendo ese valor en la ecuación correspondiente a la dirección normal:

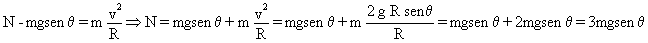
N=3mgsenθ

Para evitar el deslizamiento cuando la partícula se deposita sobre la cinta, la partícula debe de llegar al punto B con una velocidad igual a la de la cinta transportadora. Entonces:

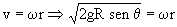
En el punto B:

θ=90^º ⇒ sen θ=1

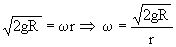
También podríamos haber determinado la velocidad de la partícula en cualquier punto de la trayectoria teniendo en cuenta que el trabajo realizado por las fuerzas que actúan sobre ella durante el desplazamiento se invierte en variar su energía cinética. Como N no realiza trabajo puesto que es perpendicular al desplazamiento, la única fuerza que realiza trabajo es el peso. El trabajo del peso será:

W_P=mgRsenθ

y es igual a la variación de energía cinética. Dado que la energía cinética inicial es nula (parte del reposo) la variación de energía cinética será únicamente la energía cinética final:

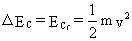
Entonces igualando:

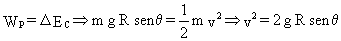
que es lo mismo que habíamos obtenido antes.