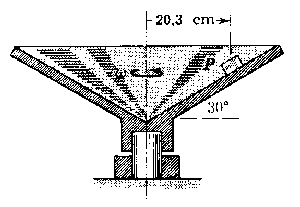
3.376 rad/s < ω < 7.157 rad/s

El peso deslizará sobre la cazoleta en dos situaciones. Cuando la cazoleta está en reposo o gira lentamente deslizará hacia abajo, pero si la cazoleta gira rápidamente el peso deslizará hacia arriba. En cualquiera de los dos casos las fuerzas de rozamiento se opondrán al movimiento.

Consideremos en primer lugar el caso en que la cazoleta gira lentamente y el objeto tiende a deslizar hacia abajo. Hacemos en primer lugar el diagrama de sólido libre, teniendo en cuenta que la fuerza de rozamiento debe oponerse al sentido del movimiento inminente. El movimiento del objeto será el del punto de la cazoleta donde apoya, es decir, circular y uniforme. Su aceleración por tanto sólo tendrá componente normal y valdrá ω²r en la dirección del radio de la circunferencia que describe y dirigida hacia el eje de giro.

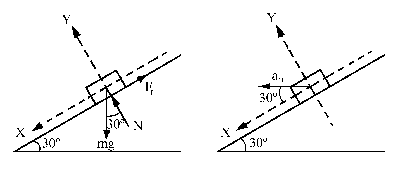
Si aplicamos la 2ª ley de Newton tenemos:

ΣF_y=ma_y ⇒ N-mgcos30^o=ma_nsen30^o ⇒ N-mgcos30^o=mω²ρ sen30^o ⇒ N=m(gcos30^o+ω²ρsen30^o)

ΣF_x=ma_x ⇒ -F_r+mgsen30^o=ma_ncos30^o ⇒ -F_r+mgsen30^o=mω²ρcos30^o ⇒

F_r=m(gsen30^o-ω²ρcos30^o)

Como el movimiento es inminente:

F_r=(F_r)_max=μN=μm(gcos30^o+ω²ρsen30^o)

Sustituyendo este valor en la ecuación del eje X:

m(gsen30^o-ω²ρcos30^o)=μm(gcos30^o+ω²ρsen30^o)

De donde:

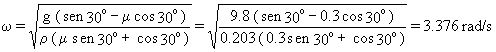
Para ese valor de ω o inferior el objeto deslizará hacia abajo.

Vamos a considerar ahora el caso en que ω sea suficientemente grande como para que el objeto tienda a deslizar hacia arriba. El diagrama del sólido libre será en este caso (hay que tener en cuenta el sentido de la fuerza de rozamiento):

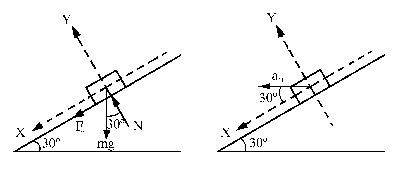
Y las ecuaciones del movimiento:

ΣF_y=ma_y ⇒ N-mgcos30^o=ma_nsen30^o ⇒ N-mgcos30^o=mω²ρsen30^o ⇒
N=m(gcos30^o+ω²ρsen30^o)

ΣF_x=ma_x ⇒ F_r+mgsen30^o=ma_ncos30^o ⇒ F_r+mgsen30^o=mω²ρcos30^o ⇒

F_r=m(ω²ρcos30^o-gsen30^o)

Por ser el movimiento inminente:

F_r=(F_r)_max=μN=μm(gcos30^o+ω²ρsen30^o)

Sustituyendo en la ecuación del eje X:

m(ω²ρcos30^o-gsen30^o)=μm(gcos30^o+ω²ρsen30^o)

De donde:

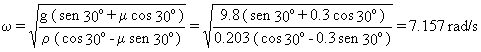
Para ω superiores a 7.157 rad/s el objeto deslizará hacia arriba. Por tanto, el intervalo en que el objeto no desliza será:

3.376 < ω < 7.157 rad/s