[t]=[P]1/2[ρ]-1/2[g]-1
ut=0.274 s
Las dimensiones de P, ρ y g son:
[ P] =MLT-2L-2=ML-1T-2; [ ρ ] =ML-3; [ g] =LT-2
La ecuación dimensional del tiempo será entonces, en función de estas variables:
[ t] =[P]α[ρ]β[g]ϒ
Y sabemos que la dimensión del tiempo es:
[ t] =T
Por tanto, igualando:
[ t] =[P]α[ρ]β[g]ϒ=T⇒ (MLT-2L-2)α ( ML-3)β ( LT-2)ϒ =T ⇒ Mα L-α T-2α Mβ L-3β Lϒ T-2ϒ =T
Como las bases son iguales, los exponentes deben ser también iguales, por lo que tendremos las tres ecuaciones:
α +β =0
-α -3β +ϒ =0
-2α -2ϒ =1
Resolviendo el sistema de tres ecuaciones y tres incógnitas obtenemos:
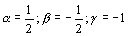
Con lo cual tendremos la ecuación dimensional del tiempo sin más que sustituir:
[ t] =[P]1/2[ρ]-1/2[g]-1
La unidad del tiempo se expresará de igual forma en función de las unidades de estas magnitudes como:
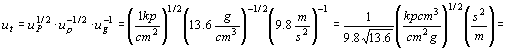
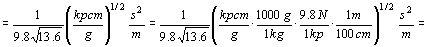
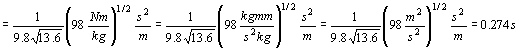
ut=0.274 s