a) t₁=3.06 s; t₂=5.36 s
b) t₁=6.12 s; t₂=10.75 s.

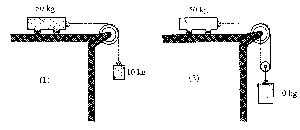
Trazamos los diagramas de sólido libre de los bloques y la polea

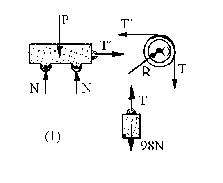
Caso (1): aplicamos la segunda ley de Newton.

En la polea el momento de las fuerzas respecto al punto O, centro de la polea, es igual al momento de inercia de la misma respecto a dicho punto O por su aceleración angular:

Σ M₀=I₀ α ⇒ T´r-Tr =(1/2)m_pr²α=0, porque m_p es despreciable, por tanto T´=T

ΣF=ma

En el bloque:

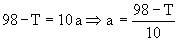
En el vagón tenemos:

2 N – P= m_c a_y= 0

T´= T = m a_x = 50 a

Las aceleraciones del vagón y del bloque son iguales en módulo ya que la cuerda que los une es inextensible .Su longitud permanece constante, si la llamamos l tendremos: l=x_c+y, siendo x_c la posición del vagón respecto al centro de la polea, que es un punto fijo e y la posición del bloque respecto al mismo punto. Derivando dos veces respecto al tiempo obtenemos: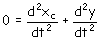

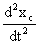es la aceleración del vagón y 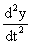es la del bloque

Sustituyendo en la ecuación:

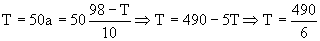
Esa fuerza T es la causa del cambio de velocidad que experimenta el vagón

Ahora aplicamos el teorema del impulso: F dt = m dv

a)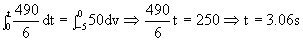

b)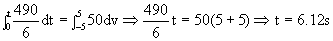

En la situación (2),  ahora el diagrama de sólido libre es:

Para la polea pequeña tenemos: T-T₁-T₂= m a= 0 porque su masa es despreciable

T₂r – T₁r = (1/2) mr^2a = 0 (por la misma razón) ⇒ T₂=T₁

Sustituyendo en la primera ecuación nos queda:

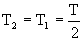
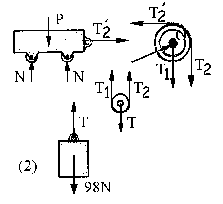Para la polea grande: T´₂r – T₂r = (1/2) m r²α=0 ⇒ T´₂=T₂ y,

por tanto T´₂= (T/2)

En el bloque:

98 – T= 10 a ⇒ T= 98 – 10 a

 

En el vagón: T´₂= (T/2)=50 a´

Ahora para hallar la relación entre a y a´ tenemos:

l=x+2y y derivando dos veces respecto al tiempo:

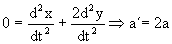
(T/2)=50 a´=100 a ⇒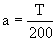

y sustituyendo en la ecuación: T= 98 – 10 a

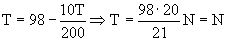
Aplicamos el teorema del impulso

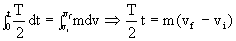
a)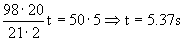

b)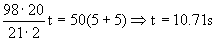

También podríamos haber resuelto el problema aplicando las ecuaciones del movimiento uniformemente acelerado en vez del teorema del impulso.