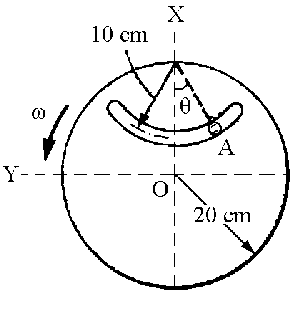
a) vA=70j cm/s; aA=-310i+200j cm/s2
b) R=0.069 N
a) La velocidad de A será:
vA=vO+ω X OA+vr
Como el punto O es un punto fijo:
vO=0
Con lo cual nos queda:
vA=ω X OA+vr
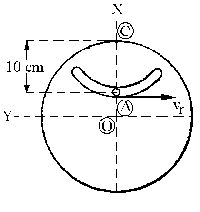
Tendremos los vectores:
w =10k; OA=10i
La velocidad relativa es la que tiene el pasador A en el sistema de referencia del disco. Dentro del disco el pasador A realiza un movimiento en el interior de la ranura; será por tanto un movimiento circular cuyo centro de curvatura es C y del que conocemos los valores de 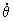 y
y 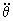 , por lo que la velocidad relativa será tangente a la trayectoria en el punto dado y valdrá:
, por lo que la velocidad relativa será tangente a la trayectoria en el punto dado y valdrá:
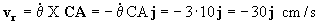
Y la velocidad de A:
vA=ω X OA+vr=(10k) X (10i)-30j=100j-30j=70 cm/s
vA=70 cm/s
La aceleración de A:
aA=aO+a X OA-ω 2OA+2ω X vr+ar
Como el punto O es un punto en reposo:
aO=0
Con lo cual nos queda:
aA=a X OA-ω 2OA+2ω X vr+ar
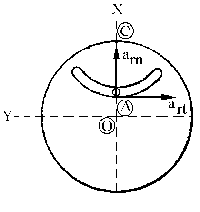
Tendremos en cuenta que la aceleración relativa tendrá dos componentes, la tangencial y la normal, es decir:
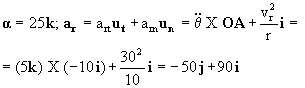
Sustituyendo todo nos queda la ecuación:
aA=a X OA-ω 2OA+2ω X vr+ar= (25k) X (10i)-102·10i+2(10k) X (-30j)-50j+90i=-310i+200j
aA=-310i+200j cm/s2
b) En el Sistema Internacional tendremos que la aceleración del pasador A es:
aA=-310i+200j cm/s2=-3.1i+2j m/s2
Hacemos entonces el diagrama de sólido libre del pasador, y lo comparamos con el diagrama de aceleraciones para este mismo pasador.
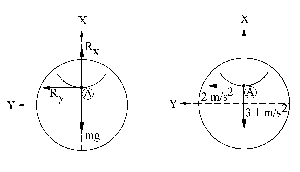
Es obvio que si la aceleración tiene dos componentes, la fuerza también debe tener dos componentes. Aplicando la segunda ley de Newton tendremos:
S Fy=maAy ⇒ Ry=0.01·2=0.02 N
S Fx=maAx ⇒ Rx-mg=-maAx
Rx=mg-maAx=m(g-aAx)=0.01(9.8-3.1)=0.067 N
La reacción valdrá entonces:
R=Rxi+Ryj=0.067i+0.02j N ⇒ 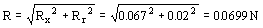
R=0.069 N
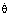 =3 rad/s,
=3 rad/s,  =5 rad/s2, ω=10 rad/s y
=5 rad/s2, ω=10 rad/s y  =25 rad/s2: a) la velocidad y aceleración del pasador A; b) la fuerza que la ranura ejerce sobre el pasador.
=25 rad/s2: a) la velocidad y aceleración del pasador A; b) la fuerza que la ranura ejerce sobre el pasador.