vB=1.98 m/s
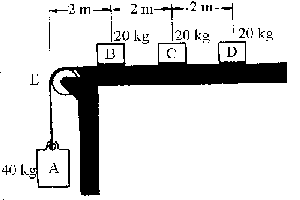
Tomaremos para todo el problema el eje X horizontal y hacia la derecha y el eje Y vertical y hacia arriba.
Aislamos el bloque B, la cinta y el paquete A y hacemos los diagramas de sólido libre correspondientes.
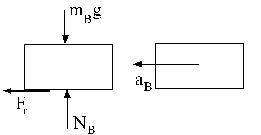
En el bloque B aplicando la segunda ley de Newton tendremos:
ΣFY=mBaBY ⇒ NB-mBg=0 ⇒ NB=mBg=20 × 9.8=196 N
ΣFX=mBaBX ⇒ Fr=mBaB
siendo aB la aceleración absoluta del paquete B, que valdrá:
aB=aCin+aB/Cin
Supongamos que la fuerza de rozamiento máxima entre el paquete y la cinta es suficientemente grande como para que no exista movimiento relativo entre el paquete y la cinta, en cuyo caso:
aB/Cin=0 ⇒ aCin=aB=aA=aC=aD
Aislamos ahora la cinta junto con los paquetes:
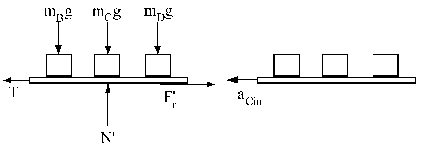
Suponemos que la masa de la cinta es despreciable frente a la masa de los paquetes. Para este sistema aplicamos también la segunda ley de Newton:
ΣFX=(mB+mC+mD)aCinX ⇒ T-Fr´=(mB+mC+mD)aCin
ΣFY=(mB+mC+mD)aCinY ⇒ N´-(mB+mC+mD)g=0 ⇒ N´=(mB+mC+mD)g=(20+20+20)9.8=588 N
Como sí existe movimiento de la cinta sobre la superficie horizontal:
Fr´=(Fr´)máx=fN´=0.50 × 588=294 N
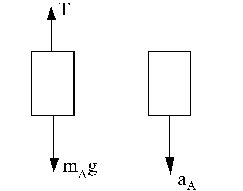
Y en el bloque A:
ΣFY=mAaBY ⇒ mAg-T=mAaA=mAaCin
Tendremos el sistema formado por las ecuaciones:
T-Fr´=(mB+mC+mD)aCin ⇒ T-294=(20+20+20)aCin
mAg-T=mAaCin ⇒ 20 × 9.8-T=20aCin
De la resolución de este sistema obtenemos:
aCin=0.981 m/s2; T=352.8 N
Habría que comprobar la suposición inicial de que los paquetes no deslizan respecto de la cinta. El valor máximo que puede alcanzar la fuerza de rozamiento entre los paquetes y la cinta es:
(Fr)máx=fNB=0.5 × 196=98 N
Ahora tendremos que en el paquete B:
Fr=mBaB=mBaCin=20 × 0.981=19.62 N
Como este valor de Fr necesario para que no exista deslizamiento del paquete sobre la cinta es inferior al de (Fr)máx la suposición inicial es correcta.
La velocidad con que cae el paquete por el punto B es por tanto la velocidad que lleva la cinta. Esta velocidad podemos determinarla teniendo en cuenta que el trabajo realizado por las fuerzas que actúan sobre la cinta se invierte en variar su energía cinética. La normal N´ y los pesos no realizan trabajo puesto que son perpendiculares al desplazamiento. Realizan trabajo la tensión T y la fuerza de rozamiento Fr´. Teniendo en cuenta que la velocidad inicial es nula y que el desplazamiento es de 2 m:
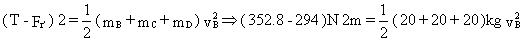
De donde:
vB=1.98 m/s
También podríamos haber utilizado las ecuaciones del movimiento uniformemente acelerado, ya que la aceleración es constante. Tendríamos en este caso:
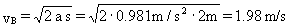
que es lo mismo que hemos obtenido.