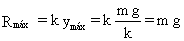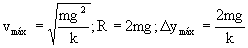
Como sólo actúan fuerzas conservativas (el peso y la fuerza elástica del muelle) se conserva la energía mecánica:

E_Pg+E_Pe+E_C=cte

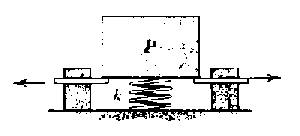
Aplicamos la conservación de la energía entre la posición que llamaremos 1, justo cuando se retiran las dos piezas, y la situación 2 cuando la velocidad del peso sea máxima. Como nivel de energía potencial cero tomaré el punto en que la velocidad es máxima. Al retirar las dos piezas (posición 1) la energía cinética es cero (se parte del reposo), la potencial elástica es cero (nos dicen que el resorte está sin deformar) y sólo tendremos energía potencial gravitatoria correspondiente a una altura y. En la posición 2 tendremos energía cinética (correspondiente a la velocidad máxima), energía potencial elástica (correspondiente a una compresión y) y no tendremos energía potencial gravitatoria:

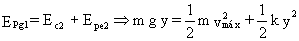
Si la velocidad es máxima, la energía cinética es máxima. Este valor se alcanzará para un valor de y tal que la derivada de la energía cinética sea nula (condición de máximo):

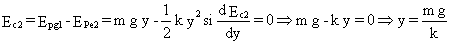
Sustituyendo este valor de la elongación en la ecuación en que habíamos aplicado la conservación de la energía:

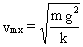
Cuando la deformación del muelle es máxima se anula la velocidad ya que:

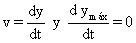
Aplico en este caso la conservación de la energía entre la misma posición inicial 1 cuando se retiran las dos piezas y la posición final que llamaré 3 en que la compresión es máxima. El nivel arbitrario de energía potencial nulo será la posición más baja del bloque. En la posición 1 por tanto sólo tendremos energía potencial gravitatoria correspondiente a la altura y_máx, mientras que en la posición 3 sólo tendremos energía potencial elástica debida a la compresión y_máx. Me quedará entonces:

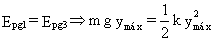
De donde:

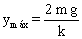
La fuerza transmitida al suelo por el muelle, R, es máxima cuando la deformación es máxima, luego: