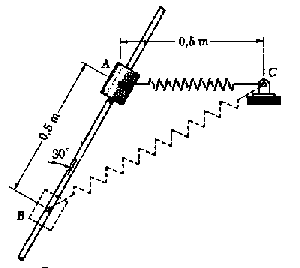
vB=2.37 m/s; a=1.69 m/s2
Si aislamos la deslizadera y hacemos el diagrama del sólido libre tendremos el sistema que se muestra en la figura.
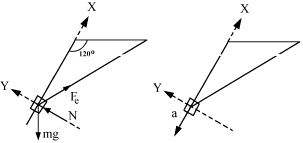
De las fuerzas que actúan sobre la deslizadera, la normal (N) no realiza trabajo por ser perpendicular al desplazamiento y las otras dos, la recuperadora del muelle (Fe) y el peso son conservativas.
Tendremos entonces que se conserva la energía mecánica entre las posiciones A y B:

Vamos a calcular ahora cada uno de los términos de la ecuación. La diferencia de alturas entre las posiciones A y B valdrá:
hA-hB=0.5cos30o=0.433 m; Δl=BC-AC
P ara calcular BC aplico el teorema del seno:
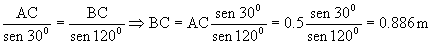
Δl=BC-AC=0.886-0.5=0.386 m
Sustituyendo todo en la ecuación de conservación de la energía:

De donde obtenemos:
vB=2.37 m/s
Para determinar la aceleración aplicamos la segunda ley de Newton a partir del diagrama del sólido libre:
ΣFX=maX⇒-mgcos30o+k(Δl)cos30o=-ma⇒-7kg×9.8cos30o+150×0.386cos30o m =-7a
a=1.69 m/s2