v=575.1 m/s
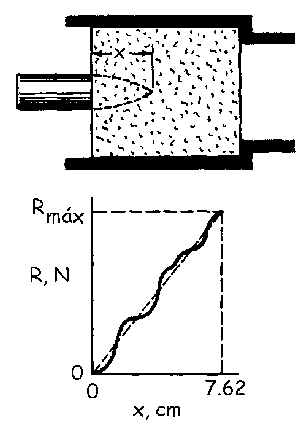
Vamos a buscar la expresión que nos dé la fuerza R en función de la penetración x. Tenemos la ecuación de una recta que pasa por el origen, luego será del tipo:
R=Cx
siendo C la pendiente de la recta. Para determinar esa constante C nos bastaría con conocer el valor de R y de x en un punto cualquiera. Para ello aplicamos la conservación de la energía, entre un instante que llamaremos 1, cuando se dispara la bala con una velocidad de 610 m/s, y el instante 2 en que el proyectil se para después de penetrar el material 7.62 cm. El movimiento es horizontal, luego tomaremos la altura del proyectil como el nivel de energía potencial gravitatoria nulo. En este caso, en la posición 1 sólo tendremos energía cinética, y en la posición 2 no habrá ni energía potencial ni cinética, ya que el proyectil se para. Nos quedará:
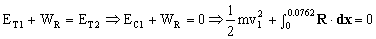
Los vectores R y dx tienen la misma dirección pero sentido contrario, luego su producto escalar será:
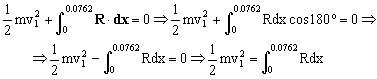
Teniendo en cuenta la expresión de R:

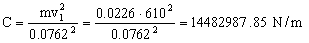
Luego la fuerza de resistencia vale:
R=Cx=14482987.85x
Ahora aplicamos la conservación de la energía entre el mismo instante anterior 1, y otro que llamaremos 3 cuando el proyectil ha penetrado 2.54 cm, en cuyo instante el proyectil tiene energía cinética ya que aún no se ha parado. Obtenemos:
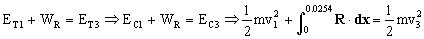
Igual que antes, los vectores R y dx tienen la misma dirección y sentido contrario luego:
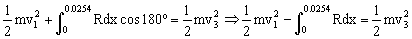
Y teniendo en cuenta la expresión de R:
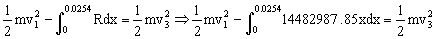
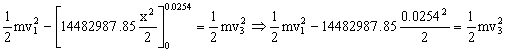
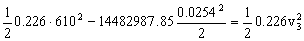
De donde obtenemos:
v3=575.1 m/s